Pada bahasan kali ini akan dibahas aplikasi integral yaitu cara menghitung luas bidang datar yang mencakup : 1) Luas daerah diatas sumbu x, 2) Luas daerah di bawah sumbu x, dan 3) Luas daerah diantara dua kurva. Untuk lebih jelasnnya perhatikan bahasan berikut ini
A. LUAS DAERAH DIATAS SUMBU X
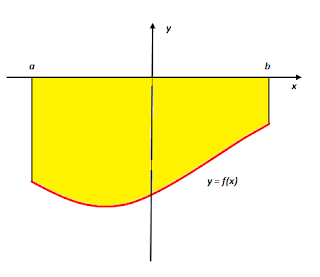
Perhatikan gambar berikut
Andaikan y = f(x) menentukan persamaan sebuah kurva dibidang xy dan andaikan f kontinu dan tidak negatif pada selang . Luas daerah yang diarsir atau luas daerah yang dibatasi oleh kurva y = f(x), x = a, x = b dan y = 0 dirumuskan dengan
Contoh Soal dan Pembahasan
Hitunglah luas daerah kurva berikut
1. , x = 2, sumbu x dan sumbu y
Pembahasan
Gambar kurva dari fungsi diatas adalah
Satuan Luas
2. dan sumbu x
Pembahasan
Gambar kuva dari fungsi diatas adalah
Luas daerah yang diarsir adalahUntuk menyelesaikan bentuk diatas dengan cepat gunakan rumus berikut
maka :
Satuan luas
Coba perhatikan gambar dan hasil perhitungan diatas, luas tersebut merupakan luas dari setengah lingkaran dengan pusat (0,0) dan jari-jari 3.
B. LUAS DAERAH DIBAWAH SUMBU X
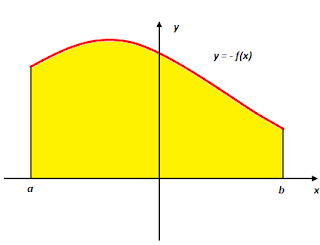
Perhatikan gambar berikut
Andaikan y = f(x) menentukan persamaan sebuah kurva dibidang xy dan andaikan f kontinu dan negatif pada selang . Karena luas daerah selalu bernilai positif maka Luas daerah yang diarsir atau luas daerah yang dibatasi oleh kurva y = f(x), x = a, x = b dan y = 0 dirumuskan dengan
Dan jika digambarkan kurvanya akan menjadi seperti ini
Contoh Soal dan Pembahasan
Hitunglah luas daerah yang dibatasi oleh kurva berikut
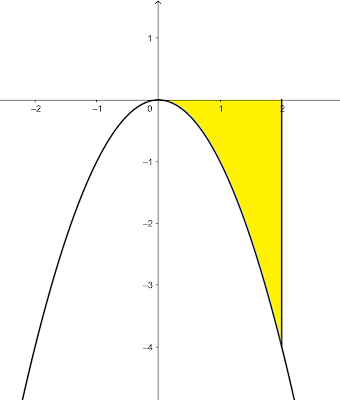
1. , sumbu y, sumbu x dan x = 2
Pembahasan
Gambar kurva dari fungsi adalah
Luas daerah yang diarsir adalah
Satua luas
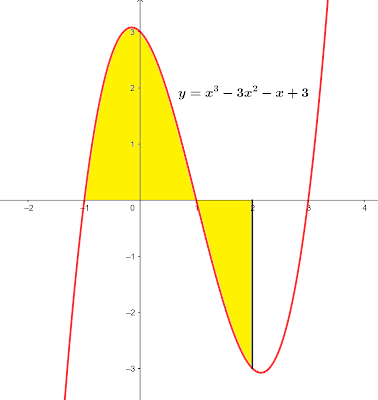
2. , sumbu x diantara x = -1 dan x = 2
Pembahasan
Gambar kurva dari fungsi diatas adalah
Satuan luas
C. LUAS DAERAH DIANTARA DUA KURVA
Perhatikan gambar berikut
Luas daerah yang diarsir adalah
Contoh Soal dan Pembahasan
Hitunglah luas daerah diantara kurva berikut
1. ,
, diantara x = -2 dan x = 2
Pembahasan
Gambar kurva dari fungsi diatas adalah
Dari gambar diatas luas daerah yang diarsir adalah
satuan luas
2. dan
Pembahasan
Gambar kurva dari fungsi diatas adalah
Langkah pertama : Mencari titik potong kedua grafik yang akan menjadi batasan nilai x yaitu
x = -2 atau x = 1
Langkah kedua : Menghitung luas antar kurva
Luas daerah yang diarsir adalah
satuan luas
3. dan
Pembahasan
Gambar kurva dari fungsi diatas adalah
Langkah pertama : Menentukan titik potong kedua kurva
x = 3 atau x = -2
Langkah kedua : menghitung luas daerah antara dua kurva
satuan luas
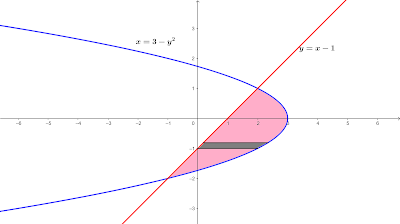
4. dan
Pembahasan
Gambar kurva dari fungsi diatas adalah
Dari bentuk kurva diatas kurang tepat mengurangkan kedua fungsi dengan partisi vertikal, akan lebih tepat mengurangkan kedua fungsi dalam partisi horizontal sehingga kita akan mengubah bentuk fungsinya ke variabel y yaitu
dan
Langkah pertama : mencari titik potong kurva dalam y
y = -2 atau y = 1
Langkah kedua : menghitung luas daerah yang diarsir
satuan luas
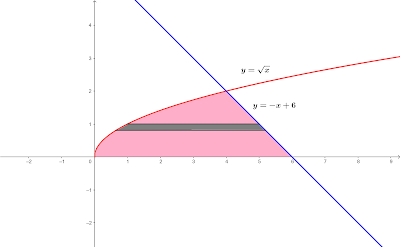
5. dan
Pembahasan
Gambar kurva dari fungsi diatas adalah
Langkah pertama : Seperti pada soal no. 4 akan dicari titik potong kedua kurva dalam variabel y
y = -3 atau y = 2
Perhatikan bahwa titik potong y = -3 tidak memenuhi karena kurva tidak akan pernah bernilai negatif. Maka batas nilai y untuk penghitungan luas daerah yang ditanyakan adalah y = 0 dan y = 2 seperti terlihat pada gambar kurva diatas.
Langkah kedua : Menghitung luas daerah yang diarsir
satuan luas
Demikian pembahasan integral untuk menghitung luas daerah bidang datar, semoga bermanfaat. Amiin.








Post a Comment
Terimakasih untuk anda telah berkomentar di postingan ini