Aplikasi Integral Untuk Menghitung Volume Benda Putar

Aplikasi dari integral adalah untuk menghitung luas daerah yang dibatasi oleh kurva yang sudah dibahas pada postingan sebelum ini, selain itu aplikasi dari integral ini untuk menghitung volume dari benda yang dibentuk oleh kuva yang diputar terhadap sumbu x, sumbu y atau keadaan tertentu yang diberikan. Untuk lebih jelasnya simaklah pembahasan dari apikasi integral untuk menghitung volume benda putar yang dibentuk dari kurva berikut ini.

VOLUME BENDA PUTAR YANG DIBATASI OLEH SEBUAH KURVA

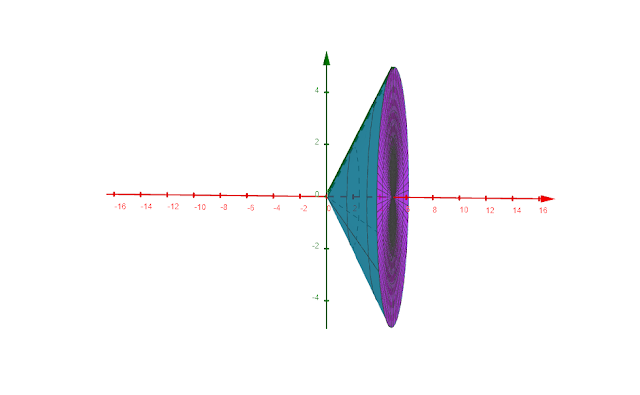
Perhatikan gambar berikut

Gambar diatas merupakan benda putar yang dibatasi oleh kurva $y=x,0\leq x\leq 5$ , sumbu x dan diputar mengelilingi sumbu x sejauh $360^{o}$ . Gambar diatas dibuat menggunakan aplikasi geogebra.

Volume benda yang terjadi dari daerah yang dibatasi oleh y = f(x), garis x = a dan x = b diputar mengelilingi sumbu x sejauh $360^{o}$ adalah

$V=\pi \int_{a}^{b}y^{2}dx$

Gambar diatas merupakan benda putar yang dibatasi oleh kurva $y=x,0\leq x\leq 5$ , sumbu y dan diputar mengelilingi sumbu y sejauh $360^{o}$ . Gambar diatas dibuat menggunakan aplikasi geogebra.

Volume benda yang terjadi dari daerah yang dibatasi oleh x = f(y), garis y = c dan y = d diputar mengelilingi sumbu y sejauh $360^{o}$ adalah

$V=\pi \int_{c}^{d}x^{2}dy$

VOLUME BENDA PUTAR YANG DIBATASI OLEH DUA BUAH KURVA

Perhatikan gambar berikut

Gambar diatas merupakan benda putar yang dibatasi oleh kurva $y=\frac{1}{4}x^{2},0\leq x\leq 4$ dan $y=x^{2},0\leq x\leq 2$ , sumbu x dan diputar mengelilingi sumbu x sejauh $360^{o}$ . Gambar diatas dibuat menggunakan aplikasi geogebra.

Volume benda yang terjadi dari daerah yang dibatasi oleh $y_{1}=f(x)$ , $y_{2}=g(x)$ , garis x = a dan x = b dengan $\left|f(x) \right|\geq \left|g(x) \right|$ diputar mengelilingi sumbu x sejauh $360^{o}$ adalah

$V=\pi \int_{a}^{b}\left ( y_{1}^{2}-y_{2}^{2} \right )dx$

Gambar diatas merupakan benda putar yang dibatasi oleh kurva $y=\frac{1}{4}x^{2},0\leq x\leq 4$ dan $y=x^{2},0\leq x\leq 2$ , sumbu y dan diputar mengelilingi sumbu y sejauh $360^{o}$ . Gambar diatas dibuat menggunakan aplikasi geogebra.

Volume benda yang terjadi dari daerah yang dibatasi oleh $x_{1}=f(y)$ , $x_{2}=g(y)$ , garis y = c dan y = d dengan $\left|f(y) \right|\geq \left|g(y) \right|$ diputar mengelilingi sumbu y sejauh $360^{o}$ adalah

$V=\pi \int_{c}^{d}\left ( x_{1}^{2}-x_{2}^{2} \right )dy$

Contoh Soal dan Pembahasan

Tentukan volume daerah yang dibatasi oleh kurva

1. $y=x^{2}-2x$ dengan sumbu x apabila diputar mengeliling sumbu x sejauh $360^{o}$

Pembahasan

Langkah 1 : menentukan batas-batas nilai x integral

$x^{2}-2x=0$

$x\left ( x-2 \right )=0$

x = 0 atau x = 2

Langkah 2 : Menghitung volume benda putar dengan rumus diatas

$V=\pi \int_{a}^{b}y^{2}dx$

$=\pi \int_{0}^{2}\left ( x^{2}-2x \right )^{2}dx$

$=\pi \int_{0}^{2}\left ( x^{4}-4x^{3}+4x^{2} \right )dx$

$=\pi \left [ \frac{1}{5}x^{5}-x^{4}+\frac{4}{3}x^{3} \right ]_{0}^{2}$

$=\pi \left (\frac{32}{5}-16+\frac{32}{5}-0 \right )$

$=\frac{16}{15}\pi$ satuan volume

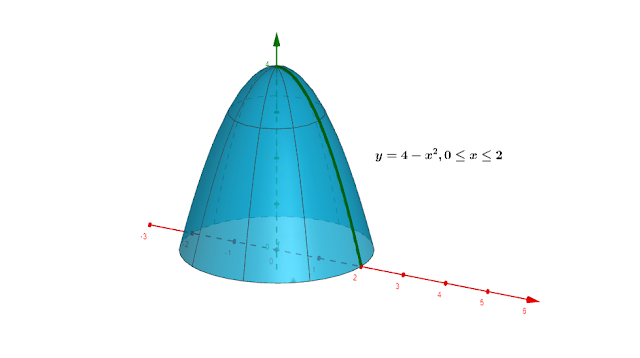
Jika kurva diatas digambar menggunakan aplikasi geogebra, maka akan diperoleh bentuk benda putar dari kurva diatas adalah (Menarik kan bentuknya ?)

Baca Juga :

Kumpulan rumus lengkap integral

Aplikasi integral untuk menghitung luas daerah bidang datar

Integral substitusi dengan bentuk trigonometrik

Integral parsial dan pembahasan soal

Integral substitusi dan pembahasan soal

Rumus dasar integral tak tentu fungsi aljabar dan pembahasan soal

2. $y=\sin x, 0\leq x\leq \pi$ dan sumbu x diputar mengeliling sumbu x sejauh $360^{o}$

Pembahasan

Batas nilai x adaah $0\leq x\leq \pi$ , maka volume benda putar dari fungsi diatas adalah

$V=\pi \int_{a}^{b}y^{2}dx$

$=\pi \int_{0}^{\pi }\left ( \sin x \right )^{2}dx$

ingat bahwa $\cos 2x=1-2\sin^{2}x\to \sin^{2}x=\frac{1}{2}-\frac{1}{2}\cos2x$ , sehingga

$=\pi \int_{0}^{\pi }\left ( \frac{1}{2}-\frac{1}{2}\cos 2x \right )dx$

$=\pi \left [ \frac{1}{2}x -\frac{1}{4}\sin 2x\right ]_{0}^{\pi }$

$=\pi \left [ \left ( \frac{1}{2}\pi -\frac{1}{4}\sin 2\pi \right )-\left ( \frac{1}{2}\left ( 0 \right )-\frac{1}{4}\sin 0 \right ) \right ]$

$=\pi \left ( \frac{\pi }{2}-0 \right )$

$=\frac{1}{2}\pi^{2}$ Satuan volume

Jika kurva diatas digambarkan menggunakan aplikasi geogebra diperoleh gambar sebagai berikut

3. $y=x^{2}$ , y = 4 dan diputar mengelilingi sumbu y sejauh $360^{o}$

Pembahasan

Karena kurva $y=x^{2}$ diputar mengelilingi sumbu y maka akan diubah persamaan tersebut ke variabel y yaitu $x=\sqrt{y}$

Volume benda putarnya adalah

$V=\pi \int_{c}^{d}x^{2}dy$

$=\pi \int_{0}^{4}\left ( \sqrt{y} \right )^{2}dy$

$=\pi \int_{0}^{4}ydy$

$=\pi \left [ \frac{1}{2}y^{2} \right ]_{0}^{4}$

$=\pi \left ( \frac{1}{2}16-0 \right )$

$=4\pi$ Satuan volume

Jika kurva diatas digambar menggunakan aplikasi geogebra adakan diperoleh gambar sebagai berikut

4. $y=4-x^2,0\leq x\leq 2$ jika diputar : a) mengelilingi sumbu x sejauh $360^{o}$ dan b) mengelilingi sumbu sejauh $360^{o}$

Pembahasan

a) $y=4-x^2,0\leq x\leq 2$ diputar mengelilingi sumbu x sejauh $360^{o}$

Gambar kurva dari fungsi diatas adalah

Volume dari benda putar diatas adalah

$V=\pi \int_{a}^{b}y^{2}dx$

$=\pi \int_{0}^{2}\left ( 4-x^2 \right )^{2}dx$

$=\pi \int_{0}^{2}\left ( 16-8x^{2}+x^{4} \right )dx$

$=\pi \left [ 16x-\frac{8}{3}x^{3}+\frac{1}{5}x^{5} \right ]_{0}^{2}$

$=\pi \left [ \left ( 32-\frac{8}{3}\left ( 8 \right )+\frac{1}{5}\left ( 32 \right )-0 \right )\right]$

$=\pi \left ( 32-\frac{64}{3}+\frac{32}{5}\right )$

$=\pi \left ( \frac{480-320+96}{15} \right )$

$=\pi \left ( \frac{256}{15} \right )$

$=255\frac{1}{15}\pi$ satuan volume

b) $y=4-x^2,0\leq x\leq 2$ diputar mengelilingi sumbu y sejauh $360^{o}$

Gambar kurva dari fungsi diatas adalah

Langkah 1 : Akan dicari batasan nilai y untuk integrasi

$x^{2}=4-y$

untuk x = 0, maka diperoleh y = 4 dan untuk x = 2 maka y = 0 sehingga batasan nilai y adalah y = 0 dan y = 4

Langkah 2 : Hitung volume benda putar

$V=\pi \int_{c}^{d}x^{2}dy$

$=\pi \int_{0}^{4}\left ( 4-y \right )dy$

$=\pi \left [ 4y-\frac{1}{2}y^{2} \right ]_{0}^{4}$

$=\pi \left ( 16-\frac{1}2{16} \right )$

$=8\pi$ Satuan volume

5. $x-2y=0$ , parabola $y^{2}=4x$ mengeliling sumbu x sejauh $360^{o}$

Pembahasan

Langkah 1 : menentukan titik potong kedua kurva

$\frac{1}{2}x=2\sqrt{x}$

$\frac{1}{4}x^{2}=4x$

$\frac{1}{4}x^{2}-4x=0$

$x^{2}-16x=0$

$x\left ( x-16 \right )=0$

x = 0 atau x = 16

gambar kurvanya adalah

Volume benda putarnya adalah

$V=\pi \int_{a}^{b}\left ( y_{1}^{2}-y_{2}^{2} \right )dx$

$=\pi \int_{0}^{16}\left ( 4x-\left ( \frac{1}{2}x \right )^{2} \right )dx$

$=\pi \int_{0}^{16}\left ( 4x-\frac{1}{4}x^{2} \right )dx$

$=\pi \left [ 2x^{2}-\frac{1}{12}x^{3} \right ]_{0}^{16}$

$=\pi \left ( 2\left ( 16^{2} \right )-\frac{1}{12}\left ( 16 \right )^{3} \right )$

$=\pi \left ( 16 \right )^{2}\left ( 2-\frac{16}{12} \right )$

$=\pi \left ( 16 \right )^{2}\left (\frac{8}{12} \right )$

$=\pi \left ( 256 \right )\left (\frac{2}{3} \right )$

$=\frac{512\pi }{3}$ satuan volume

Demikian pembahasan aplikasi integral untuk menghitung volume benda putar, semoga bermanfaat. Amiin.

Aplikasi Integral Untuk Menghitung Volume Benda Putar

VOLUME BENDA PUTAR YANG DIBATASI OLEH SEBUAH KURVA

VOLUME BENDA PUTAR YANG DIBATASI OLEH DUA BUAH KURVA

Contoh Soal dan Pembahasan

Post a Comment

Post a Comment

Contact Form

Aplikasi Integral Untuk Menghitung Volume Benda Putar

VOLUME BENDA PUTAR YANG DIBATASI OLEH SEBUAH KURVA

VOLUME BENDA PUTAR YANG DIBATASI OLEH DUA BUAH KURVA

Contoh Soal dan Pembahasan

You might like

Post a Comment

Post a Comment

Contact Form