Menghitung Jarak Titik Ke Bidang Pada Bangun Ruang

Definisi jarak titik ke bidang.

Jarak titik 𝑃 ke bidang α adalah panjang ruas garis 𝑃𝑄, dengan 𝑄 di bidang α dan 𝑃𝑄 tegak lurus bidang α.

Contoh Soal 1

Diketahui kubus ABCD.EFGH dengan panjang rusuk 5 cm. Tentukan jarak titik A ke bidang CDHG

Alternatif penyelesaian

Proyeksi titik A ke bidang CDHG diwakili oleh proyeksi titik A ke garis DH atau proyeksi titik A ke garis CD pada bidang CDHG yaitu titik D sehingga garis AD tegaklurus garis DH dan CD, maka jarak titik A ke bidang CDHG adalah panjang ruas garis AD.

Panjang ruas garis AD = panjang rusuk kubus = 5

Jadi jarak titik A ke bidang CDHG adalah 5 cm.

Contoh Soal 2

Diketahui kubus ABCD.EFGH dengan panjang rusuk 10 cm. Tentukan jarak titik A ke bidang BDHF.

Aternatif penyelesaian

Proyeksi titik A ke bidang BDHF diwakili oleh proyeksi titik A ke garis BD pada bidang BDHF yaitu titik P sehingga garis AP tegaklurus garis BD. Karena AP tegaklurus BD maka AP tegaklurus bidang BDHF.

Jarak titik A ke bidang BDHF adalah panjang ruas garis AP

Perhatikan segitiga BAD.

Dengan menggunakan perbandingan luas segitiga diperoleh :

 

Jadi jarak titik A ke bidang BDHF adalah  cm

Contoh Soal 3

Diketahui kubus ABCD.EFGH dengan panjang rusuk 10 cm. Tentukan jarak titik A ke bidang DHF.

Alternatif Penyelesaian

Bidang DHF terletak pada bidang yang berpotongan dengan kubus ABCD.EFGH yaitu bidang BDHF

Proyeksi titik A pada bidang DHF diwakili oleh proyeksi titik A pada bidang BDHF yaitu titik P. Sehingga jarak titik A ke bidang DHF sama dengan jarak titik A ke bidang BDHF yaitu panjang ruas garis AP.

Merujuk ke perhitungan pada contoh soal 2, maka panjang AP = 

Jadi jarak titik A ke bidang DHF adalah  cm

(Perhatikan bahwa jarak titik A ke bidang DHF bukan panjang ruas garis AD)

Contoh Soal 4

Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm. Tentukan jarak titik E ke bidang BDG.

Alternatif penyelesaian

Proyeksi titik A pada bidang BDG diwakili oleh proyeksi titik A pada garis OG yang terletak pada bidang BDG yaitu titik P sehingga EP tegak lurus OG.

Jarak titik E ke bidang BDG adalah panjang ruas garis EP.

Perhatikan segitiga EOG.

Panjang garis-garis yang sudah diketahui adalah OQ = 6 dan

Selanjutnya akan dicari panjang garis EO atau OG dimana EO = OG.

Perhatikan segitiga EQO

Perhatikan bahwa 

Dengan perbandingan luas segitiga diperoleh :

Jadi jarak titik E ke bidang BDG adalah  cm.

Contoh Soal 5

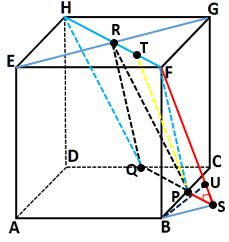
Diketahui kubus ABCD.EFGH dengan panjang rusuk 4 cm. Jika titik P di tengah-tengah rusuk BC, titik Q di tengah-tengah rusuk CD dan titik R adalah perpotongan diagonal EG dan FH. Tentukan jarak titik B ke bidang PQR.

Alternatif penyelesaian

Bidang yang memuat bidang PQR yang berpotongan dengan kubus ABCD.EFGH adalah PQHF.

Perpanjang garis QP sampai dengan titik S, sedemikian hingga PS = TF

Tarik garis dari titik F ke titik S dan tegaklurus PS.

Tarik garis dari titik B ke titik S dimana BS tegak lurus FS

Proyeksi titik B pada garis FS adalah titik U.

Jarak titik B ke bidang PQR adalah jarak titik B ke garis FS yaitu panjang ruas garis BU

(Perhatikan bahwa titik U berada di luar kubus ABCD.EFGH)

Dari soal dan gambar diketahui :

dimana 

Perhatikan segitiga BPF

Perhatikan segitiga FSP

Perhatikan segitiga FBS

Dengan menggunakan perbandingan luas segitiga diperoleh :

Jadi jarak titik B ke bidang PQR adalah  cm.

Materi ini juga saya lengkapi dengan video pembelajaran berikut (Mohon di Like dan Subscribe ya):

Baca Juga : Jarak titik ke titik pada bangun ruang Menghitung jarak titik ke garis pada bangun ruang dengan cara kesamaan luas segitiga Menghitung jarak titik ke garis pada bangun ruang menggunakan aturan cosinus Pembahasan soal jarak titik ke bidang pada bangun ruang Soal dan pembahasan jarak titik ke titik pada bangun ruang Soal dan pembahasan jarak titik ke garis pada bangun ruang Pembahasan soal jarak titik ke bidang pada bangun ruang Jarak garis ke garis pada bangun ruang Jarak garis ke bidang pada bangun ruang Cara menghitung jarak bidang ke bidang pada bangun ruang