Pembahasan Soal Fungsi Aljabar, Komposisi Fungsi dan Invers

Fungsi aljabar merupakan materi wajib yang diajarkan pada mata pelajaran matematika wajib kelas 10 SMA/MA/SMK dengan batasan kajiannya adalah, Pengertian fungsi, Daerah Asal dan Daerah Hasil, operasi pada fungsi aljabar, komposisi fungsi dan invers fungsi. Pada postingan kali ini tidak membahas pendalaman materi dari bahasan ini, karena sudah dibahas pada postingan sebelumnya yang dapat dipelajari dari link diatas. Pada postingan kali ini akan dibahas kumpulan pembahasan soal fungsi aljabar, komposisi fungsi dan invers fungsi yang pernah keluar pada ujian sekolah (US), Ujian Nasional (UN), UMPTN, SBMPTN, UTBK dan Ujian masuk perguruan tinggi lainnya. Berikut pembahasan Soal Fungsi Aljabar, Komposisi Fungsi dan Invers Fungsi :

Soal-soal Fungsi Aljabar, Komposisi Fungsi dan Invers serta pembahasannya

1. Daerah asalah fungsi $https://latex.codecogs.com/svg.image?f(x)=\frac{\sqrt{2x+6}}{3x+9}$ adalah ....

A. $https://latex.codecogs.com/svg.image?\left\{x\, |\, x\geqslant -3,x\neq 2,x\in R \right\}$

B. $https://latex.codecogs.com/svg.image?\left\{x\, |\, x\geqslant -2,x\neq 2,x\in R \right\}$

C. $https://latex.codecogs.com/svg.image?\left\{x\, |\, x\geqslant -4,x\neq -3,x\in R \right\}$

D. $https://latex.codecogs.com/svg.image?\left\{x\, |\, x\geqslant -3,x\in R \right\}$

E. $https://latex.codecogs.com/svg.image?\left\{x\, |\, x> -3,x\in R \right\}$

Pembahasan

Yang harus diperhatikan untuk menentukan daerah asal suatu fungsi rasional $https://latex.codecogs.com/svg.image?h(x)=\frac{f(x)}{g(x)}$ adalah :

1. Tentukan batasan f(x) terdefinisi, f(x) boleh sama dengan nol

2. Tentukan batasan g(x) terdefinisi dan g(x) tidak boleh sama dengan nol

Dari soal diatas

1. Perhatikan pembilang. Tentukan batasan x sehingga f(x) terdefinisi

$https://latex.codecogs.com/svg.image?\sqrt{2x+6}$ terdefinisi jika

$https://latex.codecogs.com/svg.image?2x+6\geq 0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 2x\geq -6$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x\geq -3$

2. Perhatikan penyebut

3x + 9 terdefinisi di semua $https://latex.codecogs.com/svg.image?x\in R$ dan

$https://latex.codecogs.com/svg.image?3x+9\neq 0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 3x\neq -9$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x\neq -3$

Jadi daerah asal dari fungsi diatas adalah

$https://latex.codecogs.com/svg.image?D_{f}=\left\{x\, |\, x\geqslant -3,x\neq -3,x\in R \right\}$

Kunci jawaban : Tidak ada yang benar

2. Daerah asal fungsi $https://latex.codecogs.com/svg.image?f(x)=\frac{\sqrt{2x+5}}{3x+2}$ adalah ....

A. $https://latex.codecogs.com/svg.image?\left\{x\, |\, x\neq -\frac{5}{2},x\in R \right\}$

B. $https://latex.codecogs.com/svg.image?\left\{x\, |\, x\geq \frac{5}{2},x\neq -\frac{2}{3},x\in R \right\}$

C. $https://latex.codecogs.com/svg.image?\left\{x\, |\, x\geq -\frac{5}{2},x\neq -\frac{2}{3},x\in R \right\}$

D. $https://latex.codecogs.com/svg.image?\left\{x\, |\, x\neq -\frac{2}{3},x\in R \right\}$

E. $https://latex.codecogs.com/svg.image?\left\{x\, |\, x\geq -\frac{2}{3},x\in R \right\}$

Pembahasan

1. Perhatikan pembilang

$https://latex.codecogs.com/svg.image?\sqrt{2x+5}$ terdefinis jika

$https://latex.codecogs.com/svg.image?2x+5\geq 0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 2x\geq -5$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x\geq -\frac{5}{2}$

2. Perhatikan penyebut

3x+2 terdefinisi di semua $https://latex.codecogs.com/svg.image?x\in R$ dan

$https://latex.codecogs.com/svg.image?3x+2\neq 0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 3x\neq -2$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x\neq -\frac{2}{3}$

Jadi daerah asalnya adalah

$https://latex.codecogs.com/svg.image?D_{f}=\left\{x\, |\, x\geq -\frac{5}{2},x\neq -\frac{2}{3},x\in R \right\}$

Kunci jawaban : C

3. Agar fungsi $https://latex.codecogs.com/svg.image?h(x)=\sqrt{\frac{x^{2}-16}{x}}$ terdefinisi, maka daerah asal fungsi tersebut adalah ....

A. $https://latex.codecogs.com/svg.image?\left\{x\, |\, -4\leq x< 0\,\, \mathrm{atau}\, \, x\geq 4,x\in R \right\}$

B. $https://latex.codecogs.com/svg.image?\left\{x\, |\, -4\leq x< 0\,\, \mathrm{atau}\, \, x> 4,x\in R \right\}$

C. $https://latex.codecogs.com/svg.image?\left\{x\, |\, -4\leq x\leq 0\,\, \mathrm{atau}\, \, x\geq 4,x\in R \right\}$

D. $https://latex.codecogs.com/svg.image?\left\{x\, |\, -4< x\leq 0\,\, \mathrm{atau}\, \, x> 4,x\in R \right\}$

E. $https://latex.codecogs.com/svg.image?\left\{x\, |\, -4\leq x\leq 4,x\in R \right\}$

Pembahasan

$https://latex.codecogs.com/svg.image?h(x)=\sqrt{\frac{x^{2}-16}{x}}$ terdefinisi jika $https://latex.codecogs.com/svg.image?\frac{x^{2}-16}{x}\geq 0$ dan $https://latex.codecogs.com/svg.image?x\neq 0$

1. $https://latex.codecogs.com/svg.image?\frac{x^{2}-16}{x}\geq 0$ jika $https://latex.codecogs.com/svg.image?x^{2}-16\geq 0$ dan x > 0

$https://latex.codecogs.com/svg.image?x^{2}-16\geq 0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x^{2}-16\geq 0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( x+4 \right )\left ( x-4 \right )\geq 0$

Pembuat nol fungsi

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( x+4 \right )\left ( x-4 \right )= 0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x=-4\, \, \mathrm{atau}\, \, x=4$

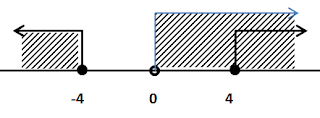
Masukkan nlai x ke garis bilangan

Nilai x yang memenuhi adalah $https://latex.codecogs.com/svg.image?x\geq 4$ (Perhatikan nilai x yang memenuhi adalah nilai x di daerah yang memiliki arsiran paling banyak)

2. $https://latex.codecogs.com/svg.image?\frac{x^{2}-16}{x}\geq 0$ jika $https://latex.codecogs.com/svg.image?x^{2}-16\leq 0$ dan x < 0

$https://latex.codecogs.com/svg.image?x^{2}-16\leq 0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( x+4 \right )\left ( x-4 \right )\leq 0$

Pembuat nol fungsi

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( x+4 \right )\left ( x-4 \right )= 0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x=-4\, \, \mathrm{atau}\, \, x=4$

Masukkan nilai x ke garis bilangan

Nilai x yang memenuhi adalah $https://latex.codecogs.com/svg.image?-4\leq x<0$

Jika digabung kedua nilai x diatas maka diperoleh daerah asal dari fungsi h(x) adalah

$https://latex.codecogs.com/svg.image?D_{h}=\left\{x\, |\, -4\leq x< 0\,\, \mathrm{atau}\, \, x\geq 4,x\in R \right\}$

Kunci jawaban : A

4. Daerah hasil fungsi $https://latex.codecogs.com/svg.image?f(x)=2x^{2}-2x-12$ untuk daerah asal $https://latex.codecogs.com/svg.image?\left\{x\, |\, -3\leq x\leq 0,x\in R \right\}$ adalah ....

A. $https://latex.codecogs.com/svg.image?\left\{y\, |\, y\leq 12,y\in R \right\}$

B. $https://latex.codecogs.com/svg.image?\left\{y\, |\, y\geq -12\frac{1}{2},y\in R \right\}$

C. $https://latex.codecogs.com/svg.image?\left\{y\, |\, y\geq -12,y\in R \right\}$

D. $https://latex.codecogs.com/svg.image?\left\{y\, |\, -12\leq y\geq 12,y\in R \right\}$

E. $https://latex.codecogs.com/svg.image?\left\{y\, |\, -12\frac{1}{2}\leq y\geq 12,y\in R \right\}$

Pembahasan

Substitusi batas-batas nilai x daerah asal ke fungsi f(x)

$https://latex.codecogs.com/svg.image?x=-3\Rightarrow f(3)=2(-3)^{2}-2(-3)-12=18+6-12=12$

$https://latex.codecogs.com/svg.image?x=0\Rightarrow f(0)=2(0)^{2}-2(0)-12=-12$

Jadi daerah hasil fungsi f(x) adalah $https://latex.codecogs.com/svg.image?R_{f}=\left\{y\, |\, -12\leq y\leq 12,y\in R \right\}$

Kunci jawaban : D

5. Agar fungsi $https://latex.codecogs.com/svg.image?h(x)=\sqrt{\frac{x^{2}+5x+6}{x-5}}$ terdefinisi, daerah asal fungsi tersebut adalah ....

A. $https://latex.codecogs.com/svg.image?\left\{x\, |\, -3\leq x\leq -2\, \, \mathrm{atau}\, \, x>5,x\in R \right\}$

B. $https://latex.codecogs.com/svg.image?\left\{x\, |\, x\leq -3\, \, \mathrm{atau}\, \, x\geq 5,x\in R \right\}$

C. $https://latex.codecogs.com/svg.image?\left\{x\, |\, -2\leq x\leq 3\, \, \mathrm{atau}\, \, x> 5,x\in R \right\}$

D. $https://latex.codecogs.com/svg.image?\left\{x\, |\, -3\leq x\leq 2\, \, \mathrm{atau}\, \, x> 5,x\in R \right\}$

E. $https://latex.codecogs.com/svg.image?\left\{x\, |\, -3\leq x\leq 5,x\in R \right\}$

Pembahasan

$https://latex.codecogs.com/svg.image?h(x)=\sqrt{\frac{x^{2}+5x+6}{x-5}}$ terdefinisi jika $https://latex.codecogs.com/svg.image?\frac{x^{2}+5x+6}{x-5}\geq 0$ dan $https://latex.codecogs.com/svg.image?x\neq 5$

1. $https://latex.codecogs.com/svg.image?\frac{x^{2}+5x+6}{x-5}\geq 0$ jika $https://latex.codecogs.com/svg.image?x^{2}+5x+6\geq 0$ dan $x-5>0$

$https://latex.codecogs.com/svg.image?x^{2}+5x+6\geq 0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( x+2 \right )\left ( x+3 \right )\geq 0$

Pembuat nol fungsi

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( x+2 \right )\left ( x+3 \right )= 0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x=-2\, \, \mathrm{atau}\, \, x=-3$

$x-5>0$

$x>5$

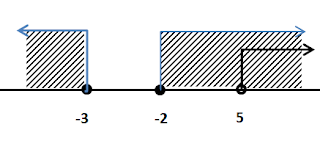
Masukkan nilai -nilai x ke garis bilangan

Nilai x yang memenuhi adalah x > 5

2. $https://latex.codecogs.com/svg.image?\frac{x^{2}+5x+6}{x-5}\geq 0$ jika $https://latex.codecogs.com/svg.image?x^{2}+5x+6\leqslant 0$ dan $x-5<0$

$https://latex.codecogs.com/svg.image?x^{2}+5x+6\leqslant 0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( x+2 \right )\left ( x+3 \right )\leqslant 0$

Pembuat nol fungsi

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( x+2 \right )\left ( x+3 \right )= 0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x=-2\, \, \mathrm{atau}\, \, x=-3$

x - 5 < 0

x < 5

Masukkan semua nilai x ke garis bilangan

Nilai x yang memenuhi adalah $https://latex.codecogs.com/svg.image?-3\leq x\leq -2$

Jika kedua interval diatas digabungkan maka daerah asal dari fungsi h(x) adalah

$https://latex.codecogs.com/svg.image?D_{h}=\left\{x\, |\, -3\leq x\leq -2\, \, \mathrm{atau}\, \, x>5,x\in R \right\}$

Kunci jawaban : A

6. Diketahui f(x) = 3 - x dan $https://latex.codecogs.com/svg.image?g(x)=x^{2}+2x$ . Fungsi komposisi (fog)(x) adalah....

A. $https://latex.codecogs.com/svg.image?\left ( f\, o\, g \right )(x)=x^{2}-4x+15$

B. $https://latex.codecogs.com/svg.image?\left ( f\, o\, g \right )(x)=x^{2}+4x+15$

C. $https://latex.codecogs.com/svg.image?\left ( f\, o\, g \right )(x)=x^{2}-4x-15$

D. $https://latex.codecogs.com/svg.image?\left ( f\, o\, g \right )(x)=x^{2}-8x+15$

E. $https://latex.codecogs.com/svg.image?\left ( f\, o\, g \right )(x)=x^{2}-8x-15$

Pembahasan

$https://latex.codecogs.com/svg.image?\left ( f\, o\, g \right )(x)=f(g(x))$

$https://latex.codecogs.com/svg.image?=f(x^{2}+2x)$

$https://latex.codecogs.com/svg.image?=3-\left ( x^{2}+2x \right )$

$https://latex.codecogs.com/svg.image?=3-x^{2}-2x$

$https://latex.codecogs.com/svg.image?=-x^{2}-2x+3$

Kunci Jawaban : Tidak ada yang benar

7. Diketahui f(x) = 8x - 2 dan $https://latex.codecogs.com/svg.image?g(x)=x^{2}-x-6$ . Fungsi komposisi (fog)(x) adalah....

A. $https://latex.codecogs.com/svg.image?\left ( f\, o\, g \right )(x)=8x^{2}-8x-48$

B. $https://latex.codecogs.com/svg.image?\left ( f\, o\, g \right )(x)=8x^{2}-8x+48$

C. $https://latex.codecogs.com/svg.image?\left ( f\, o\, g \right )(x)=8x^{2}-8x-50$

D. $https://latex.codecogs.com/svg.image?\left ( f\, o\, g \right )(x)=8x^{2}-8x+50$

E. $https://latex.codecogs.com/svg.image?\left ( f\, o\, g \right )(x)=8x^{2}+8x-50$

Pembahasan

$https://latex.codecogs.com/svg.image?\left ( f\, o\, g \right )(x)=f(g(x))$

$https://latex.codecogs.com/svg.image?=f(x^{2}-x-6)$

$https://latex.codecogs.com/svg.image?=8(x^{2}-x-6)-2$

$https://latex.codecogs.com/svg.image?=8x^{2}-8x-48-2$

$https://latex.codecogs.com/svg.image?=8x^{2}-8x-50$

Kunci jawaban : C

8. Fungsi $https://latex.codecogs.com/svg.image?f:R\rightarrow R$ dan $https://latex.codecogs.com/svg.image?g:R\rightarrow R$ . Jika g(x) = x - 1 dan $https://latex.codecogs.com/svg.image?(f\, o\, g)(x)=x^{3}-4x$ , nilai dari f(2) = ....

A. 9

B. 13

C. 15

D. 17

E. 25

Pembahasan

$https://latex.codecogs.com/svg.image?(f\, o\, g)(x)=x^{3}-4x$

$https://latex.codecogs.com/svg.image?f(g(x))=x^{3}-4x$

$https://latex.codecogs.com/svg.image?f(x-1)=x^{3}-4x$

Misal p = x - 1, maka x = p + 1, sehingga diperoleh

$https://latex.codecogs.com/svg.image?f(p)=(p+1)^{3}-4(p+1)$

$https://latex.codecogs.com/svg.image?f(2)=(2+1)^{3}-4(2+1)$

$https://latex.codecogs.com/svg.image?=(3)^{3}-4(3)$

$=27-12=15$

Kunci jawaban : C

9. Diketahui fungsi $https://latex.codecogs.com/svg.image?f:R\rightarrow R$ dan $https://latex.codecogs.com/svg.image?g:R\rightarrow R$ . Jika diketahui $https://latex.codecogs.com/svg.image?(f\, o\, g)(x)=x^{3}-6x^{2}+10x-3$ dan g(x) = x - 2, nilai dari f(2) adalah ....

A. 0

B. 1

C. 4

D. 5

E. 8

Pembahasan

$https://latex.codecogs.com/svg.image?(f\, o\, g)(x)=x^{3}-6x^{2}+10x-3$

$https://latex.codecogs.com/svg.image?f(g(x))=x^{3}-6x^{2}+10x-3$

$https://latex.codecogs.com/svg.image?f(x-2)=x^{3}-6x^{2}+10x-3$

misal p = x - 2, maka x = p + 2

$https://latex.codecogs.com/svg.image?f(p)=(p+2)^{3}-6(p+2)^{2}+10(p+2)-3$

$https://latex.codecogs.com/svg.image?f(2)=(2+2)^{3}-6(2+2)^{2}+10(2+2)-3$

$https://latex.codecogs.com/svg.image?=(4)^{3}-6(4)^{2}+10(4)-3$

$=64-96+40-3=5$

Kunci jawaban : D

10. Proses pembuatan meja diproses melalui 2 tahap yaitu tahap pengolahan dan finishing. Setelah tahap pengolahan bahan menjadi model meja kemudian dilakukan tahap finishing. Pada tahap finishing, model meja yang terbentuk dipoleh menjadi meja yang siap dijual. Proses dalam tahap pengolahan mengikuti fungsi f(x) = 3x - 70 dan tahap finishing mengikuti fungsi $https://latex.codecogs.com/svg.image?g(x)=x^{2}$ . Jika tersedia bahan 50 lembar kayu, banyak meja yang dapat dibuat adalah....

A. 2.500

B. 3.900

C. 6.400

D. 12.800

E. 19.200

Pembahasan

Kasus diatas merupakan kasus komposisi fungsi. Karena tahap finishing mengikuti fungsi g(x) maka

$https://latex.codecogs.com/svg.image?(g\, o\, f)(x)=g(f(x))$

$=g(3x-70)$

$https://latex.codecogs.com/svg.image?=(3x-70)^{2}$

$https://latex.codecogs.com/svg.image?x=50\Rightarrow (g\, o\, f)(50)=(3(50)-70)^{2}$

$https://latex.codecogs.com/svg.image?=(150-70)^{2}$

$https://latex.codecogs.com/svg.image?=(80)^{2}=6.400$

Kunci jawaban : C

11. Suatu pabrik kertas dengan bahan dasar kayu (x) memproduksi kertas melalui dua tahap. Tahap pertama menggunakan mesin I menghasilkan kertas setengah jadi (m) dengan mengikuti fungsi $https://latex.codecogs.com/svg.image?m=f(x)=x^{2}-3x-2$ . Tahap kedua menggunakan mesin II menghasilkan kertas mengikuti fungsi g(m) = 4m + 2, dengan x dan m dalam satuan ton. Jika bahan dasar kayu yang tersedia untuk suatu produksi sebesar 4 ton, banyak kertas yang dihasilkan adalah ....

A. 5 ton

B. 10 ton

C. 15 ton

D. 20 ton

E. 30 ton

Pembahasan

Kasus diatas mengikuti komposisi (g o f)(x) sehingga diperoleh

$https://latex.codecogs.com/svg.image?(g\, o\, f)(x)=g(f(x))$

$https://latex.codecogs.com/svg.image?=g(x^{2}-3x-2)$

$https://latex.codecogs.com/svg.image?=4(x^{2}-3x-2)+2$

Banyak bahan dasar kayu yang tersedia adalah 4 ton (x = 4). Substitusi x = 4 ke fungsi (gof)(x), sehingga diperoleh :

$https://latex.codecogs.com/svg.image?x=4\Rightarrow (g\, of)(4)=4(4^{2}-3(4)-2)+2$

$=4(16-12-2)+2$

$=4(2)+2=8+2=10$

Jadi banyak kertas yang dihasilkan adalah 10 ton

Kunci jawaban : B

12. Diketahui $https://latex.codecogs.com/svg.image?f(x)=\frac{4x+1}{x-4},x\neq 4$ . Invers dari fungsi f(x) adalah ....

A. $https://latex.codecogs.com/svg.image?\frac{x+4}{4x-1},x\neq \frac{1}{4}$

B. $https://latex.codecogs.com/svg.image?\frac{x-4}{4x+1},x\neq -\frac{1}{4}$

C. $https://latex.codecogs.com/svg.image?\frac{4x-1}{x+4},x\neq -4$

D. $https://latex.codecogs.com/svg.image?\frac{4x+1}{x-4},x\neq 4$

E. $https://latex.codecogs.com/svg.image?\frac{4x-1}{x-4},x\neq 4$

Pembahasan

Rumus
$https://latex.codecogs.com/svg.image?f(x)=\frac{ax+b}{cx+d}\Rightarrow f^{-1}(x)=\frac{-dx+b}{cx-a}$

Sehingga diperoleh

$https://latex.codecogs.com/svg.image?f(x)=\frac{4x+1}{x-4},x\neq 4$ , maka

$https://latex.codecogs.com/svg.image?f^{-1}(x)=\frac{-(-4)x+1}{x-4}=\frac{4x+1}{x-4},x\neq 4$

Kunci jawaban : D

13. Diketahui $https://latex.codecogs.com/svg.image?f(x)=\frac{2x+3}{5x+4},x\neq -\frac{4}{5}$ . Invers dari fungsi f(x) adalah .....

A. $https://latex.codecogs.com/svg.image?\frac{5x-4}{2x+3},x\neq -\frac{3}{2}$

B. $https://latex.codecogs.com/svg.image?\frac{5x+4}{2x-3},x\neq \frac{3}{2}$

C. $https://latex.codecogs.com/svg.image?\frac{2x+3}{5x-4},x\neq \frac{4}{5}$

D. $https://latex.codecogs.com/svg.image?\frac{-4x+3}{5x-2},x\neq \frac{2}{5}$

E. $https://latex.codecogs.com/svg.image?\frac{4x-3}{5x-2},x\neq \frac{2}{5}$

Pembahasan

$https://latex.codecogs.com/svg.image?f(x)=\frac{2x+3}{5x+4},x\neq -\frac{4}{5}\Rightarrow f^{-1}(x)=\frac{-4x+3}{5x-2},x\neq \frac{2}{5}$

Kunci jawaban : D

14. Diketahui fungsi $https://latex.codecogs.com/svg.image?f(x)=\sqrt{2x+3},x\geq -\frac{3}{2}$ . Jika $https://latex.codecogs.com/svg.image?f^{-1}(x)$ adalah invers dari fungsi f(x), nilai dari $https://latex.codecogs.com/svg.image?f^{-1}(3)$ adalah .....

A. 6

B. 3

C. $https://latex.codecogs.com/svg.image?\frac{3}{2}$

D. $https://latex.codecogs.com/svg.image?-\frac{1}{2}$

E. -1

Pembahasan

Cara 1

$https://latex.codecogs.com/svg.image?y=\sqrt{2x+3}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow y^{2}=2x+3$

$https://latex.codecogs.com/svg.image?\Leftrightarrow y^{2}-3=2x$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x=\frac{y^{2}-3}{2}$

Sehingga diperoleh

$https://latex.codecogs.com/svg.image?f^{-1}(x)=\frac{x^{2}-3}{2}$

$https://latex.codecogs.com/svg.image?x=3\Rightarrow f^{-1}(3)=\frac{3^{2}-3}{2}=\frac{9-3}{2}=\frac{6}{2}=3$

Cara 2

Menggunakan rumus
$https://latex.codecogs.com/svg.image?f(x)=\sqrt[n]{ax+b}\Rightarrow f^{-1}(x)=\frac{x^{n}-b}{a}$

Sehingga diperoleh

$https://latex.codecogs.com/svg.image?f(x)=\sqrt{2x+3}\Rightarrow f^{-1}(x)=\frac{x^{2}-3}{2}$

Kunci jawaban : B

15. Diketahui $https://latex.codecogs.com/svg.image?f(x)=\frac{x+3}{2x-1},x\neq \frac{1}{2}$ dan $https://latex.codecogs.com/svg.image?f^{-1}(x)$ adalah invers dari f(x). Nilai dari $https://latex.codecogs.com/svg.image?f^{-1}(-3)$ adalah ....