Cara Menentukan Nilai Maksimum dan Minimum Fungsi Aljabar

NILAI MAKSIMUM DAN MINIMUM FUNGSI ALJABAR

Salah satu penggunaan turunan fungsi adalah untuk menentukan nilai minimun dan maksimum fungsi. Untuk membahas topik ini. perhatikan gambar berikut.

Dari gambar diatas, perhatikan sifat berikut

Misalkan f adalah fungsi bernilai real yang kontinu dan memiliki turunan pertama dan kedua pada $x_{1}\in I$ , sehingga

Jika $f'(x_{1})=0$ , maka titik $(x_{1},f(x_{1}))$ disebut titik stasioner/titik kritis/titik balik
Jika $f'(x_{1})=0$ dan $f''(x_{1})>0$ , maka titik $(x_{1},f(x_{1}))$ disebut titik balik minimum fungsi
Jika $f'(x_{1})=0$ dan $f''(x_{1})<0$ , maka titik $(x_{1},f(x_{1}))$ disebut titik balik maksimum fungsi
Jika $f''(x_{1})=0$ , maka titik $(x_{1},f(x_{1}))$ disebut titik belok fungsi

Contoh Soal dan Pembahasan

Contoh soal 1

Jika $\frac{d}{dx}\left [ f(x) \right ]=f'(x)$ adalah turunan pertama fungsi f(x) dan $\frac{d}{dx}\left [ f'(x) \right ]=f''(x)$ adalah turunan keduanya, maka tentukan turunan kedua fungsi-fungsi berikut

1. f(x) = 3x - 2

Jawab

f '(x) = 3x

f ''(x) = 3

2. $f(x)=-2x^{2}-x$

Jawab

$f'(x)=-4x-1$

$f''(x)=-4$

3. $f(x)=-x^{4}+2x^{2}-4$

Jawab

$f'(x)=-4x^{3}+4x$

$f''(x)=-12x^{2}+4$

4. $f(x)=\left ( 3x-2 \right )^{2}$

Jawab

$f'(x)=2\left ( 3x-2 \right ).3=6(3x-2)=18x-12$

$f''(x)=18$

5. $f(x)=\frac{2x}{x+1}$

Jawab

$f'(x)=\frac{2(x+1)-2x.1}{\left ( x+1 \right )^{2}}=\frac{2}{\left ( x+1 \right )^{2}}$

$f''x)=\frac{0.(x+1)^{2}-2.2x}{\left ( x+1 \right )^{4}}=\frac{-4x}{\left ( x+1 \right )^{4}}$

Contoh Soal 2

Tentukan nilai maksimum dan nilai minimum jika ada fungsi-fungsi berikut

1. $fx)=x^{2}-2x$

Jawab

Langkah 1. Menentukan pembuat nol fungsi

Fungsi f(x) memotong sumbu x jika f(x) = 0

$x^{2}-2x=0$

x(x - 2) = 0

x = 0 atau x - 2 = 0

x = 2

Jadi kurva memotong sumbu x di titik (0,0) dan (2,0)

Langkah 2. Menentukan interval fungsi naik dan fungsi turun

Fungsi naik jika f '(x) > 0

2x - 2 > 0

2x > 2

x > 1

Fungsi turun jika f '(x) < 0

2x - 2 < 0

2x < 2

x < 1

Jadi interval fungsi naik adalah {x | x > 1 dengan x bilangan real}

Interval fungsi turun adalah {x |x < 1 dengan x bilangan real}

Langkah 3 : Menentukan titik stasioner

Titik stasioner diperoleh jika f '(x) = 0

$f'(x)=2x-2=0$

2x = 2

x = 1

Substitusikan x = 1 ke fungsi f(x)

$x=1\to f(1)=1^{2}-2.1=1-2=-1$

Jadi titik stasioner fungsi $fx)=x^{2}-2x$ adalah (1, -1)

Langkah 4. Menentukan jenis titik stasioner

Cara 1. Uji jenis titik stasioner juga dapat dilakukan dengan uji selang yaitu

Dari Uji selang terlihat bahwa pada x = 1 gradien = 0 dan merupakan nilai absis yang menyebabkan fungsi bernilai minimum, maka

$x=1\to f(1)=1^{2}-2.1=1-2=-1$

Jadi nilai minimum fungsi adalah f(1) = -1

Cara 2 : Turunan kedua

Kita akan uji titik stasioner ke turunan kedua yaitu jika f ''(x) > 0 maka titik (x,f(x)) adalah titik balik minimum fungsi

f ''(x) = 2

f ''(x) > 0

Karena f ''(x) > 0, maka titik (1, -1) adalah titik balik minimum

Sehingga nilai minimum fungsi $fx)=x^{2}-2x$ adalah f(1) = -1

Fungsi tidak memiliki nilai maksimum.

Jika grafik fungsi $fx)=x^{2}-2x$ digambarkan sebagai berikut

2. $f(x)=-\frac{1}{2}x^{2}+\frac{2}{3}x-\frac{3}{4}$

Jawab

Langkah 1 : Menentukan pembuat nol fugsi

Akan dicek nilai diskriminannya apakah grafik memotong sumbu x atau tidak

$D=b^{2}-4ac$

$=\left ( \frac{2}{3} \right )^{2}-4\left ( -\frac{1}{2} \right )\left ( -\frac{3}{4} \right )$

$=\frac{4}{9}- \frac{3}{2}$

$=\frac{2}{18}- \frac{27}{18}$

$=\frac{8}{18}- \frac{27}{18}$

$=-\frac{19}{18}$

Karena D < 0 maka grafik tidak memotong sumbu x

Langkah 2. Menentukan interval fungsi naik dan fungsi turun

Fungsi naik jika f '(x) > 0

$-x+\frac{2}{3}>0$

$-x>-\frac{2}{3}$

$x<\frac{2}{3}$

Jadi fungsi naik pada interval {x | $x<\frac{2}{3}$ , x bilangan ril}

Fungsi turun jika f '(x) < 0

$-x+\frac{2}{3}<0$

$-x<-\frac{2}{3}$

$x>\frac{2}{3}$

Jadi fungsi turun pada interval {x | $x>\frac{2}{3}$ , x bilangan ril}

Langkah 3 : Menentukan titik stasioner

Titik stasioner atau titik balik diperoleh jika f '(x) = 0

$f'(x)=-x+\frac{2}{3}=0$

$-x=-\frac{2}{3}$

$x=\frac{2}{3}$

substitusi $x=\frac{2}{3}$ ke fungsi $f(x)=-\frac{1}{2}x^{2}+\frac{2}{3}x-\frac{3}{4}$

$x=\frac{2}{3}\to f(\frac{2}{3})=-\frac{1}{2}\left ( \frac{2}{3} \right )^{2}+\frac{2}{3}\left ( \frac{2}{3} \right )-\frac{3}{4}$

$=-\frac{1}{2}\left ( \frac{4}{9} \right )+\frac{4}{9}-\frac{3}{4}$

$=-\frac{4}{18}+\frac{4}{9}-\frac{3}{4}$

$=-\frac{8}{36}+\frac{16}{36}-\frac{27}{36}$

$=-\frac{19}{36}$

Jadi titik stasioner atau titik balik adalah $\left ( \frac{2}{3},-\frac{19}{36} \right )$

Langkah 4. Menentukan jenis titik stasioner

Cara 1 : Uji selang

Terlihat bahwa pada $x=\frac{2}{3}$ gradien = 0, titik sebelumnya gradien positif artinya grafik naik dan titik sesudahnya gradien negatif artinya grafik turun.

Sehingga dapat disimpulkan bahwa pada $x=\frac{2}{3}$ terjadi nilai f(x) maksimum, sehingga

$x=\frac{2}{3}\to f(\frac{2}{3})=-\frac{1}{2}\left ( \frac{2}{3} \right )^{2}+\frac{2}{3}\left ( \frac{2}{3} \right )-\frac{3}{4}$

$=-\frac{1}{2}\left ( \frac{4}{9} \right )+\frac{4}{9}-\frac{3}{4}$

$=-\frac{4}{18}+\frac{4}{9}-\frac{3}{4}$

$=-\frac{8}{36}+\frac{16}{36}-\frac{27}{36}$

$=-\frac{19}{36}$

Jadi $f\left ( \frac{2}{3} \right )=-\frac{19}{36}$ merupakan nilai maksimum fungsi

Cara 2 : Uji turunan kedua

Kita akan uji titik stasioner/titik balik ke turunan kedua yaitu jika f ''(x) < 0 maka titik (x,f(x)) adalah titik balik maksimum fungsi

f ''(x) = -1

f ''(x) < 0

Karena f ''(x) < 0, maka titik $\left ( \frac{2}{3},-\frac{19}{36} \right )$ adalah titik balik maksimum

Jika grafik fungsi $f(x)=-\frac{1}{2}x^{2}+\frac{2}{3}x-\frac{3}{4}$ digambarkan sebagai berikut

Aturan Pencarian Turunan dan Pembahasan Soal

Konsep Turunan Fungsi Untuk Mencari Persamaan Garis Singgung Kurva

Aplikasi Turunan Untuk Menentukan Interval Fungsi Naik dan Turun

Menghitung Kecepatan dan Percepatan Menggunakan Turunan Fungsi Aljabar

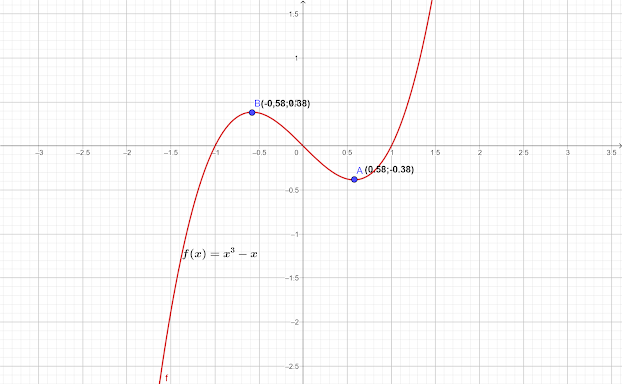
3. $f(x)=x^{3}-x$

Langkah 1 . Menentukan titik potong terhadap sumbu x

$x^{3}-x=0$

$x(x^{2}-1)=0$

$x(x-1)(x+1)=0$

x = 0 atau x = 1 atau x = -1

Jadi grafik memotong sumbu x di titik (-1,0), (0,0) dan (1,0)

Langkah 2 : Menentukan interval naik dan turun

Fungsi naik jika f '(x) > 0

$3x^{2}-1>0$

$x^{2}>\frac{1}{3}$

$x>\pm \sqrt{\frac{1}{3}}$

Perhatikan garis bilangan berikut

Jadi fungsi naik pada interval $x>\sqrt{\frac{1}{3}}$ atau $x<-\sqrt{\frac{1}{3}}$

Fungsi turun jika f '(x) < 0

$3x^{2}-1<0$

$3x^{2}<1$

$x^{2}<\frac{1}{3}$

$x<\pm \sqrt{\frac{1}{3}}$

Perhatikan garis bilangan berikut

Jadi grafik turun pada interval $-\sqrt{\frac{1}{3}}<x<\sqrt{\frac{1}{3}}$

Langkah 3 : Menentukan titik stasioner

Titik stasioner atau titik balik diperoleh jika f '(x) = 0

$f'(x)=3x^{2}-1=0$

$3x^{2}=1$

$x^{2}=\frac{1}{3}$

$x_{1,2}=\pm \sqrt{\frac{1}{3}}$

$x_{1,2}=\pm 0,58$

Substitusi $x_{1,2}=\pm \sqrt{\frac{1}{3}}$ ke persamaan $f(x)=x^{3}-x$

$x_{1}=\sqrt{\frac{1}{3}}\to f\left ( \sqrt{\frac{1}{3}} \right )=\left ( \sqrt{\frac{1}{3}} \right )^{3}-\sqrt{\frac{1}{3}}$

$=\frac{1}{3}\sqrt{\frac{1}{3}}-\sqrt{\frac{1}{3}}$

$=\sqrt{\frac{1}{3}}\left ( \frac{1}{3}-1 \right )$

$=\sqrt{\frac{1}{3}}\left ( \frac{-2}{3}\right )$

$=-\frac{2}{3}\sqrt{\frac{1}{3}}$

= - 0,38

Koordinat titik balik pertama adalah $\left ( \sqrt{\frac{1}{3}},-\frac{2}{3}\sqrt{\frac{1}{3}} \right )$ atau (0,58 ; -0,38)

$x_{2}=-\sqrt{\frac{1}{3}}\to f\left ( -\sqrt{\frac{1}{3}} \right )=\left ( -\sqrt{\frac{1}{3}} \right )^{3}+\sqrt{\frac{1}{3}}$

$=-\frac{1}{3}\sqrt{\frac{1}{3}}+\sqrt{\frac{1}{3}}$

$=\sqrt{\frac{1}{3}}\left ( -\frac{1}{3}+1 \right )$

$=\frac{2}{3}\sqrt{\frac{1}{3}}$

= 0,38

Koordinat titik balik kedua adalah $\left ( -\sqrt{\frac{1}{3}},\frac{2}{3}\sqrt{\frac{1}{3}} \right )$ atau (-0,58 ;0,38)

Langkah 4. Uji jenis titik stasioner

Aka dilakukan uji selang yaitu

Jika dilihat uji selang tersebut, maka fungsi tidak memiliki nilai maksimum ataupun nilai minimum. Tetapi jika dibatasi Daerah asalnya yaitu -1 < x < 1 maka

Nilai maksimum = $f\left ( -\sqrt{\frac{1}{3}} \right )=\frac{2}{3}\sqrt{\frac{1}{3}}=0,38$

Nilai Minimum = $f\left ( \sqrt{\frac{1}{3}} \right )=-\frac{2}{3}\sqrt{\frac{1}{3}}=-0,38$

Jika grafik fungsi $f(x)=x^{3}-x$ sebagai berikut

4. Sebuah bola dilambungkan ke atas. Jika lintasan bola berbentuk parabola dengan persamaan lintasan $h(t)=-t^{2}+t+6$ dan dengan mengabaikan percepatan gravitasi bumu dan kecepatan awal bola, hitunglah tinggi maksimal dari bola tersebut.