Konsep Turunan Untuk Mencari Persamaan Garis Singgung Kurva

Perhatikan gambar berikut

Konsep Turunan Fungsi Untuk Mencari Persamaan Garis Singgung Kurva

Sumber : Matematika SMA/MA/SMK/MAK kelas XI Kementerian Pendidikan dan Kebudayaan RI 2017

Definisi Gradien dan Persamaan Garis Singgung

Definisi 1

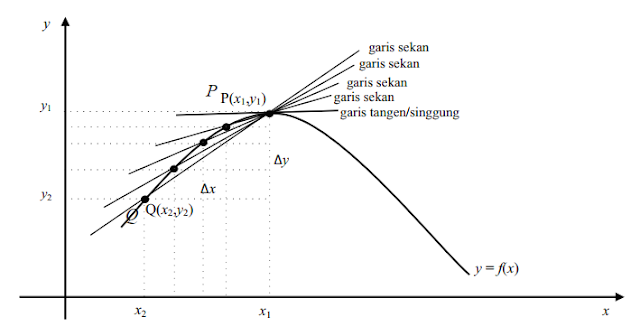
Misalkan $f:\mathbb{R}\to \mathbb{R}$ adalah fungsi kontinu dan titik $P(x_{1},y_{1})$ dan $Q(x_{1}+\bigtriangleup x,y_{1}+\bigtriangleup y)$ pada kurva f. Garis sekan menghubungkan titik P dan Q dengan persamaan gradien

$m_{sec}=\frac{f(x_{1}+\bigtriangleup x)-f(x_{1})}{\bigtriangleup x}$

Definisi 2

Misalkan f adalah fungsi kontinu bernilai real dan titik $P(x_{1},y_{1})$ pada kurva f. Gradien garis singgung di titik $P(x_{1},y_{1})$ adalah limit gradien garis secan di titik $P(x_{1},y_{1})$ , ditulis

$m_{GS}=\displaystyle \lim_{\bigtriangleup x \to 0}m_{sec}=\displaystyle \lim_{\bigtriangleup x \to 0}\frac{f(x_{1}+\bigtriangleup x)-f(x_{1})}{\bigtriangleup x}$

jika limitnya ada

Disamping itu bentuk $\displaystyle \lim_{\bigtriangleup x \to 0}\frac{f(x_{1}+\bigtriangleup x)-f(x_{1})}{\bigtriangleup x}$ merupakan turunan pertama dari fungsi f.

Perlu diingat juga rumusan dari persamaan garis singgung yang melalui titik $P(x_{1},y_{1})$ dan bergradien m adalah

$(y-y_{1})=m(x-x_{1})$

Contoh Soal dan Pembahasan

Tentukan persamaan garis singgung dengan absis x = 1 dari setiap fungsi berikut.

1. f(x) = 2x

Pembahasan

Fungsi f(x) = 2x merupakan garis lurus dengan gradien m = 2 (ingat pembahasan gradien garis lurus)

sehingga persamaan garis singgungnya berimpit dengan garis f. Jadi persamaan garis singgung sama dengan persamaan garisnya yaitu f(x) = 2x

2. $f(x)=2x^{2}$

Pembahasan

Langkah 1 : Menentukan titik singgung

$x=1\to f(1)=2.1=2$

dengan demikian diperoleh titik singgung adalah (1,2)

Langkah 2 : Menentukan gradien garis singgung

m = f'(x) = 4x

$x=1\to m=4.1=4$

dengan demikian diperoleh gradien garis singgung m = 4

Langkah 3 : Menentukan persamaan garis singgung

$(y-y_{1})=m(x-x_{1})$

y - 2 = 4(x - 1)

y - 2 = 4x - 4

y = 4x - 4 + 2

y = 4x - 2

Jadi persamaan garis singgung $f(x)=2x^{2}$ dengan absis x = 1 adalah y = 4x - 2

3. $f(x)=(2x-1)^{3}$

Pembahasan

Langkah 1 : Menentukan titik singgung

$x=1\to f(1)=(2.1-1)^{3}=1^{3}=1$

dengan demikian diperoleh titik singgung adalah (1,1)

Langkah 2 : Menentukan gradien garis singgung

$m=f'(x)=3(2x-1)^{2}2=6(2x-1)^{2}$

$x=1\to m=6(2.1-1)^{2}=6.1=6$

dengan demikian diperoleh gradien garis singgungnya adalah m = 6

Langkah 3 : Menentukan persamaan garis singgung

$(y-y_{1})=m(x-x_{1})$

y - 1 = 6(x - 1)

y - 1 = 6x - 6

y = 6x - 6 + 1

y = 6x - 5

Jadi persamaan garis singgung $f(x)=(2x-1)^{3}$ dengan absis x = 1 adalah y = 6x - 5

4. $f(x)=\frac{2}{x+1}$

Pembahasan

Langkah 1 : Menentukan titik singgung

$x=1\to f(1)=\frac{2}{1+1}=\frac{2}{2}=1$

dengan demikian diperoleh titik singgungnya adalah (1,1)

Langkah 2 : Menentukan gradien garis singgung

$m=f'(x)=\frac{u'v-uv'}{v^{2}}$

$=\frac{0.(x+1)-2.1}{(x+1)^{2}}$

$=\frac{-2}{(x+1)^{2}}$

$x=1\to m=\frac{-2}{(1+1)^{2}}=\frac{-2}{2^{2}}=-\frac{1}{2}$

dengan demikian gradien garis singgungnya adalah $m=-\frac{1}{2}$

Langkah 3 : Menentukan persamaan garis singgung

$(y-y_{1})=m(x-x_{1})$

$y-1=-\frac{1}{2}(x-1)$

$y-1=-\frac{1}{2}x+\frac{1}{2}$

$y=-\frac{1}{2}x+\frac{1}{2}+1$

$y=-\frac{1}{2}x+\frac{3}{2}$

Jadi persamaan garis singgung $f(x)=\frac{2}{x+1}$ dengan absis x = 1 adalah $y=-\frac{1}{2}x+\frac{3}{2}$

Aturan Pencarian Turunan dan Pembahasan Soal

Aplikasi Turunan Untuk Menentukan Interval Fungsi Naik dan Fungsi Turun

Aplikasi Turunan Untuk Menentukan Nilai Maksimum dan Minimum Fungsi Aljabar

Menghitung Kecepatan dan Percepatan Menggunakan Turunan Fungsi Aljabar

5. $f(x)=\frac{2}{x^{2}}$

Pembahasan

Langkah 1 : Menentukan titik singgung

$x=1\to f(1)=\frac{2}{1^{2}}=2$

dengan demikian titik singgungnya adalah (1,2)

Langkah 2 : Menentukan gradien garis singgung

$m=f'(x)=\frac{u'v-uv'}{v^{2}}$

$=\frac{0.x^{2}-2(2x)}{(x^{2})^{2}}$

$=\frac{-4x}{x^{4}}=\frac{-4}{x^{3}}$

$x=1\to m=\frac{-4}{1^{3}}=-4$

dengan demikian gradien garis singgungnya adalah m = - 4

Langkah 3 : Menentukan persamaan garis singgung

$(y-y_{1})=m(x-x_{1})$

y - 2 = -4(x - 1)

y - 2 = -4x + 4

y = -4x + 4 + 2

y = -4x + 6

Jadi persamaan garis singgung $f(x)=\frac{2}{x^{2}}$ dengan absis x = 1 adalah y = -4x + 6

6. Soal UN Tahun 2017

Diketahui grafik fungsi $y=2x^{2}-3x+7$ berpotongan dengan garis y = 4x + 1. Salah satu persamaan garis singgung yang melalui titik potong kurva dan garis tersebut adalah....

A. y = 5x + 7

B. y = 5x - 1

C. y = x + 5

D. y = 3x - 7

E. y = 3x + 5

Pembahasan

Langkah 1 : Menentukan titik potong kurva dan garis

$2x^{2}-3x+7=4x+1$

$2x^{2}-3x-4x+7-1=0$

$2x^{2}-7x+6=0$

$(2x-3)(x-2)=0$

$2x-3=0\vee x-2=0$

$2x=3$ x = 2

$x=\frac{3}{2}$

$x=\frac{3}{2}\to y=4.\frac{3}{2}+1=6+1=7$

$x=2\to y=4.2+1=8+1=9$

Jadi titik yang dilalui oleh garis singgung adalah $\left ( \frac{3}{2},7 \right )$ dan (2,9)

Langkah 2 : Menentukan gradien garis singgung

Ambil kurva $y=2x^{2}-3x+7$

m = y' = 4x -3

Gradien garis pertama yaitu gradien garis yang melalui titik $\left ( \frac{3}{2},7 \right )$

$x=\frac{3}{2}\to m_{1}=y'=4.\frac{3}{2}-3=6-3=3$

Gariden garis kedua yaitu gradien garis yang melalui titik (2,9)

$x=2\to m_{2}=y'=4.2-3=8-3=5$

Langkah 3 : Menentukan persamaan garis singgung

Persamaan garis singgung pertama yaitu garis singgung yang melalui titik $\left ( \frac{3}{2},7 \right )$ dengan gradien $m_{1}=3$

$(y-y_{1})=m_{1}(x-x_{1})$

$y-7=3\left ( x-\frac{3}{2} \right )$

$y-7=3x-\frac{9}{2}$

$y=3x-\frac{9}{2}+7$

$y=3x+\frac{5}{2}$

Peramaan garis singgung kedua yaitu garis singgung yang melalui titik (2,9) dengan gradien $m_{2}=5$

$(y-y_{1})=m_{2}(x-x_{1})$

y - 9 = 5(x - 2)

y - 9 = 5x - 10

y = 5x - 10 + 9

y = 5x - 1

Kunci Jawaban : B

7. Soal UN Tahun 2018

Persamaan garis singgung kurva $y=x^{2}-5x+12$ yang sejajar garis 3x - y + 5 = 0 adalah ....

A. 3x - y + 4 = 0

B. 3x - y - 4 = 0

C. 3x - y - 20 = 0

D. x - 3y - 4 = 0

E. x - 3y + 4 = 0

Pembahasan

Langkah 1 : Menentukan gradien garis singgung

Gradien dari garis 3x - y + 5 = 0 adalah $m=\frac{-3}{-1}=3$

Karena garis singgung kurva sejajar dengan garis 3x - y + 5 = 0, maka gradien garis singgung kurva sama dengan gradien garis singgung tersebut yaitu m = 3

Langkah 2 : Menentukan titik singgung kurva $y=x^{2}-5x+12$

m = y' = 2x - 5

$m=3\to 3=2x-5$

$2x=3+5$

$x=\frac{8}{2}=4$

substitusi x = 4 ke persamaan kurva

$x=4\to y=4^{2}-5.4+12$

= 16 - 20 + 12

= 8

sehingga diperoleh titik sunggung pada kurva adalah (4,8)

Langkah 3 : Menentukan persamaan garis singgung

$(y-y_{1})=m(x-x_{1})$

y - 8 = 3(x - 4)

y - 8 = 3x - 12

y - 3x - 8 + 12 = 0

y - 3x + 4 = 0

-y + 3x - 4 = 0

3x - y - 4 = 0

Kunci Jawaban : B

Demikian pembahasan tentang penggunaan turunan fungsi untuk menentukan gradien dari persamaan garis singgung. Semoga bermanfaat.

Konsep Turunan Untuk Mencari Persamaan Garis Singgung Kurva

Definisi Gradien dan Persamaan Garis Singgung

Contoh Soal dan Pembahasan

Post a Comment

Post a Comment

Contact Form

Konsep Turunan Untuk Mencari Persamaan Garis Singgung Kurva

Definisi Gradien dan Persamaan Garis Singgung

Contoh Soal dan Pembahasan

You might like

Post a Comment

Post a Comment

Contact Form