Cara Menentukan Interval Fungsi Naik dan Fungsi Turun

Perhatikan gambar berikut

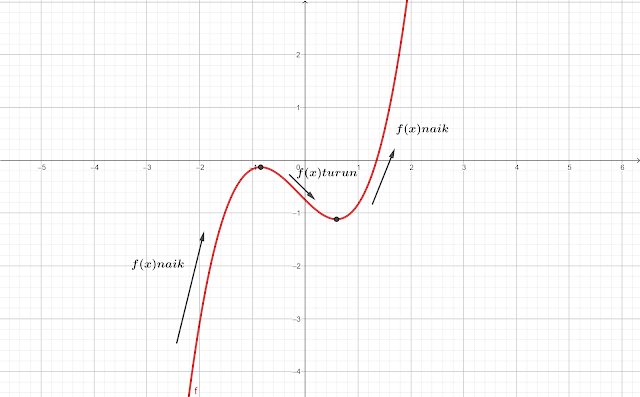Gambar dibuat menggunakan aplikasi Geogebra

Definisi Fungsi Naik dan Fungsi Turun

Misalkan fungsi  

1. Fungsi f dikatakan naik jika 
2. Fungsi f dikatakan turun jika 

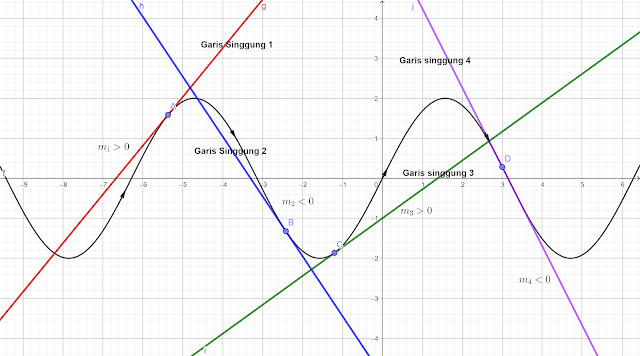
Perhatikan hubungan gradien garis singgung, fungsi naik dan turun dari gambar berikut.

Berdasarkan gambar diatas hubungan garis singgung dengan fungsi naik dan fungsi turun adalah

Garis Singgung	Gradien	f‘(x)	Menyinggung di
1	m = +	f’(x) > 0	Fungsi Naik
2	m = -	f’(x) < 0	Fungsi Turun
3	m = +	f’(x) > 0	Fungsi Naik
4	m = -	f’(x) < 0	Fungsi Turun

Sifat Turunan pada Fungsi Naik dan Turun

Misal f adalah fungsi bernilai real dan dapat diturunkan pada setiap , maka :

1. Jika f '(x) > 0 maka fungsi selalu naik pada interval I
2. Jika f '(x) < 0 maka fungsi selalu turun pada interval I
3. Jika  maka fungsi tidak pernah turun pada interval I
4. Jika  maka fungsi tidak pernah turun pada interval I

Contoh Soal dan Pembahasan

1. Tentukan interval fungsi naik dan fungsi turun dari fungsi 

Pembahasan

Syarat fungsi naik jika  f '(x) > 0, maka

4x - 3 > 0

4x > 3

Jadi fungsi naik pada interval  

Syarat fungsi turun jika  f '(x) < 0, maka

4x - 3 < 0

4x < 3

Jadi fungsi turun pada interval  

2. Tentukan interval fungsi naik dan fungsi turun dari fungsi  

Pembahasan

Langkah 1 : Menentukan interval fungsi f(x) terdefinisi (Ingat bentuk akar) 

Fungsi  akan terdefinisi jika , maka

                     x = 1

Garis bilangannya adalah

Jadi interval fungsi f terdefinisi adalah  

Langkah 2 : Menentukan interval naik dan turun

Fungsi naik jika f '(x) > 0

Perhatikan bentuk diatas akan terdefinisi jika penyebut . Dan bentuk ini tidak akan pernah bernilai negatif maka sudah pasti 

Merujuk ke perhitungan pada langkah 1 diperoleh x < 0 atau x > 1

Karena penyebut positif dan supaya  f '(x) positif maka harus 2x - 1 > 0

2x - 1 > 0

2x > 1

Masukkan semua nilai x yang diperoleh dari langkah 2 ke garis bilangan

Jadi fungsi naik pada interval 

Fungsi turun jika f '(x) < 0, maka

Perhatikan bentuk diatas akan terdefinisi jika penyebut . Dan bentuk ini tidak akan pernah bernilai negatif maka sudah pasti 

Merujuk ke perhitungan pada langkah 1 diperoleh x > 0 atau x > 1

Karena penyebut sudah pasti positif maka haruslah

2x - 1 < 0

2x < 1

Masukkan nilai x yang diperoleh pada garis bilangan

Jadi fungsi turun pada interval 

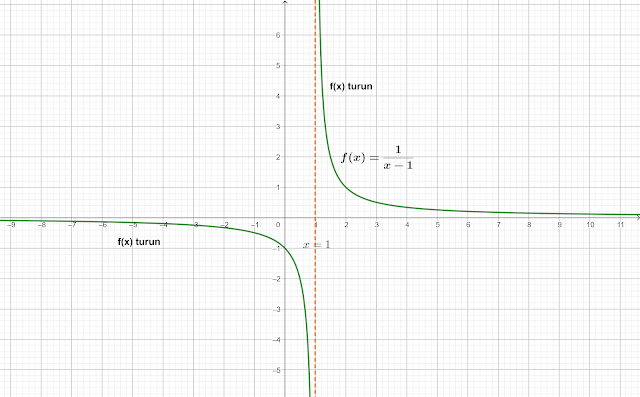
Jika kita lihat grafik fungsi dari  sebagai berikut

Baca Juga : Menyelesaikan Soal Turunan Menggunakan Definisi Turunan Aturan Pencarian Turunan dan Pembahasan Soal Konsep Turunan Fungsi Untuk Mencari Persamaan Garis Singgung Kurva Aplikasi Turunan Untuk Menentukan Nilai Maksimum dan Minimum Fungsi Aljabar Menghitung Kecepatan dan Percepatan Menggunakan Turunan Fungsi Aljabar

3. Tentukan interval fungsi naik dan fungsi turun dari 

Pembahasan

Fungsi naik jika f '(x) > 0

pertidaksamaan diatas akan terpenuhi jika < 0 sementara  tidak akan pernah bernilai negatif. Sehingga tidak ada nilai x yang memenuhi pertidaksamaan diatas. Artinya bahwa fungsi  tidak memilik interval fungsi naik.

Fungsi turun jika f '(x) < 0

pertidaksamaan diatas akan terpenuhi jika  > 0

 > 0

Pembuat nol fungsi

 = 0

x = 1

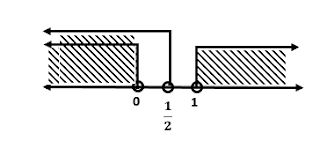
jika dibuat garis bilangannya seperti pada gambar berikut

dari garis bilangan diperoleh nilai x yang memenuhi adalah x > 1 atau x < 1

Jadi interval fungsi turun dari fungsi  adalah {x|x > 1 atau x < 1, x bilangan real}.

Jika digambarkan grafik fungsi  seperti gambar berikut

Demikian pembahasan aplikasi turunan untuk menentukan interval naik dan interval turun pada fungsi aljabar.