SOAL-SOAL BARISAN DAN DERET ARITMATIKA SERTA PEMBAHASANNYA
1. Dari barisan 3, 5, 7, 9, 11, ... suku ke 21 adalah....
A. 40
B. 43
C. 46
D. 49
E. 5
Pembahasan
Dik : a = 3, b = 5 - 3 = 2
Dit : U21 = ....?
Jawab
U21 = a + 20b
= 3 + 20 . 2
= 3 + 40
= 43
Kunci Jawaban : B
2. Suatu barisan aritmatika diketahui suku ke 4 adalah 6 dan beda 3. Suku ke 8 adalah ....
A. 18
B. 31
C. 34
D. 37
E. 40
Pembahasan
Dik : U4 = 6, b = 3
Dit : U8
Jawab
U4 = a + 3b
6 = a + 3.3
6 = a + 9
a = 6 - 9
a = -3
Maka diperoleh
U8 = a + 7b
= -3 + 7 . 3
= -3 + 21
= 18
Kunci Jawaban : A
3. Suatu barisan aritmatika diketahui suku ke 15 adalah 30 dan bedanya -5. Suku ke 6 adalah ....
A. 65
B. 25
C. 75
D. 80
E. 90
Pembahasan
Dik : U15 = 30, b = -5
Dit : U6 =.....?
Jawab
U15 = a + 14b
30 = a + 14 (-5)
30 = a + (-60)
30 = a - 60
a = 30 + 60
a = 90
Maka diperoleh
U6 = a + 5b
= 90 + 5(-5)
= 90 - 15
= 75
Kunci Jawaban : C
4. Rumus suku ke n dari barisan aritmatika 4, 9, 14, 19, 24, ... adalah ....
A. 5n + 2
B. 5n - 1
C 5n + 1
D. 5n - 2
E. 5n + 3
Pembahasan
Dik : a = 4, b = 5
Dit : Un
Jawab
Un = a + (n - 1)b
= 4 + (n - 1)5
= 4 + 5n - 5
= 5n + 4 - 5
= 5n - 1
Kunci Jawaban : B
5. Suatu barisan aritmatika diketahui suku ke 6 adalah -4 dan suku ke 9 adalah -19, maka suku ke 11 adalah ....
A. -34
B. -29
C. -19
D. -24
E. -14
Pembahasan
Dik : U6 = -4, U9 = -19
Dit : U11 = ....?
Jawab
U6 = a + 5b
-4 = a + 5b
a + 5b = -4 ..........(1)
U9 = a + 8b
-19 = a + 8b
a + 8b = -19 .....(2)
Eliminasi varabel a dari persamaan (1) dan (2)
Subtitusi b = -5 ke persamaan (1)
a + 5b = -4
a + 5(-5) = -4
a - 25 = -4
a = -4 + 25
a = 21
Sehingga diperoleh
U11 = a + 10b
= 21 + 10(-5)
= 21 - 50
= -29
Kunci Jawaban : B
6. Hasil dari 5 + 7 + 9 + 11 + ... + 41 adalah .....
A. 379
B. 437
C. 471
D. 407
E. 207
Pembahasan
Dik : a = 5, b = 7 - 5 = 2 dan Un = 41
Dit : Sn = ....?
Jawab
Un = 41
a + (n - 1)b = 41
5 + (n - 1)2 = 41
5 + 2n - 2 = 41
2n + 3 = 41
2n = 41 - 3
2n = 38
n = 38/2
n = 19
maka U19 = 41
Sehingga diperoleh
Kunci Jawaban : B
7. Jika 4 + 6 + 8 + 10 + ... + x = 130, maka nilai x adalah ....
A. 10
B. 15
C. 18
D. 22
E. 32
Pembahasan
Dik : a = 4, b = 6 - 2 = 2, Un = x dan Sn = 130
Dit : x = ....?
Jawab
Karena n = 10 maka U10 = x
U10 = x
a + 9b = x
4 + 9.2 = x
4 + 18 = x
22 = x
Kunci Jawaban : D
8. Suku keempat dari dari suatu barisan aritmatika adalah 20 dan jumlah lima suku pertamanya sama dengan 80. Jumlah sebelas suku pertamanya adalah ....
A. 196
B. 210
C. 264
D. 308
E. 332
Pembahasan
Dik : U4 = 20, S5 = 80
Dit : S11 = ....?
Jawab
U4 = 20
a + 3b = 20 ..........(1)
..........(2)
Eliminasi a dari persamaan (1) dan (2)
Substitusi b = 4 ke persamaan (1)
a + 3b = 20
a + 3.4 = 20
a + 12 = 20
a = 20 - 12
a = 8
Maka diperoleh
Kunci Jawaban : D
9. Dari suatu deret aritmatika diketahui jumlah n suku pertamanya ditentukan dengan rumus . Suku ke 6 adalah ....
A. 19
B. 33
C. 36
D. 39
E. 42
Pembahasan
Dik :
Dit : U6 = ......?
Jawab
Ambil n = 6, maka
Ambil n = 5, maka
Sementara
Kunci Jawaban : A
10. Jumlah bilangan bulat antara 10 dan 60 yang habis dibagi 3 adalah ....
A. 552
B. 486
C. 462
D. 312
E. 396
Pembahasan
Deret artimatika dari bilangan antara 10 dan 60 yang habis dibagi 3 adalah
12 + 15 + 18 + 21 + ... + 57
Dari deret aritamatika diatas :
Dik : a = 12, b = 3 dan Un = 57
Dit : Sn = .... ?
Jawab
Un = 57
a + (n - 1)b = 57
12 + (n - 1)3 = 57
12 + 3n - 3 = 57
3n + 9 = 57
3n = 57 - 9
3n = 48
n = 48/3
n = 16
Karena n = 16 maka U16 = 57 sehingga yang akan dicari adalah S16.
Kunci Jawaban : A
11. Dalam suatu barisan aritmatika jumlah suku keempat dan keenam adalah 28. Jika suku kedua barisan itu adalah 5, suku ke sembilan adalah .....
A. 19
B. 21
C. 24
D. 26
E. 28
Pembahasan
Dik : U4 + U6 = 28, U2 = 5
Dit : U9 = ....?
Jawab
U4 + U6 = 28
(a + 3b) + (a + 5b) = 28
a + a + 3b + 5b = 28
2a + 8b = 28 ........ (1)
U2 = 5
a + b = 5 ........(2)
Ubah persamaan (2) menjadi a =
a + b = 5
a = 5 - b ......(3)
Subtitusi persamaan (3) ke persamaan (1)
2a + 8b = 28
2(5 - b) + 8b = 28
10 - 2b + 8b = 28
10 + 6b = 28
6b = 28 - 10
6b = 18
b = 18/6 = 3
Subtitusi b = 3 ke persamaan (3)
a = 5 - b
a = 5 - 3
a = 2
Sehingga diperoleh
U9 = a + 8b
= 2 + 8.3
= 2 + 24
= 26
Kunci Jawaban : D
12. Jumlah semua bilangan ganjil antara 300 dan 750 yang bukan kelipatan 7 adalah .....
A. 84.000
B. 84.215
C. 84.250
D. 84.375
E. 84.500
Pembahasan
Deret bilangan ganjil antara 300 dan 750 adalah
301 + (303 + 305 + 307 + 309 + 311 + 313) + 315 + (317 + 319 + 321 + 323+ 325 + 327 ) + 329 + ....+ 735 + (737 +739 + 741 + 743 + 745 + 747) + 749
Misalkan deret diatas adalah Sx
Perhatikan deret aritmatika diatas yang didalam kurung merupakan bilangan ganjil yang bukan kelipatan 7 dan yang tidak didalam kurung merupakan bilangan ganjil yang merupakan kelipatan 7
Bilangan ganjil yang merupakan kelipan 7 membentuk sebuah deret aritmatika yaitu
301 + 315 + 329 + ... + 749 dan memiliki beda 14.
Misal
Jumlah bilangan ganjil antara 300 dan 750 yang bukan kelipatan 7 = S
Jumlah bilangan ganjil antara 300 dan 750 = Sx
Jumlah bilangan ganjil antara 300 dan 750 yang merupakan kelipatan 7 = Sy
Sehingga diperoleh
Jumlah bilangan ganjil antara 300 dan 750 bukan kelipatan 7 = Jumlah bilangan ganjil antara 300 dan 750 - Jumlah bilangan ganjil antara 300 dan 750 kelipatan 7
S = Sx - Sy
Untuk deret aritmatika Sx
301 + (303 + 305 + 307 + 309 + 311 + 313) + 315 + (317 + 319 + 321 + 323+ 325 + 327 ) + 329 + .... + (... + 747) + 749
Dik : a = 301 , b = 303 - 301 = 2 dan Un = 749
Ambil Un = 749
Un = 749
a + (n -1)b = 749
301 + (n - 1)2 = 749
(n - 1)2 = 749 - 301
(n - 1) 2 = 448
n - 1 = 448/2
n - 1 = 224
n = 224 + 1
n = 225
sehingga diperoleh
Jadi Sx = 118.125
Untuk deret aritmatika Sy
301 + 315 + 329 + ... + 749
Dik : a = 301, b = 315 - 301 = 14 dan Un = 749
Ambil Un = 749
Un = 749
a + (n - 1)b = 749
301 + (n - 1)14 = 749
(n - 1)14 = 749 - 301
(n - 1)14 = 448
n - 1 = 448/14
n - 1 = 32
n = 32 + 1 = 33
Karena n = 33 maka U33 = 749 dan akan dicari S33
Jadi Sy = 17.325
Sehingga
S = Sx - Sy
= 118.125 - 17.325
= 100.800
Kunci Jawaban : tidak ada yang benar
13. Jumlah semua bilangan asli dari 10 sampai 99 yang habis dibagi 3 tetapi tidak habis dibagi 4 adalah.....
A. 477
B. 585
C. 1.178
D. 1.233
E. 1.428
Pembahasan
Deret Bilangan Asli dari 10 sampai 99 yang habis dibagi 3 adalah
12 + (15 + 18 + 21) + 24 + (27 + 30 + 33) + 36 + ... 84 + (87 + 90 + 93) + 96 + ( 99)
Perhatikan bilangan yang tidak didalam kurung merupakan bilangan yang habis dibagi 3 dan habis dibagi 4, sementara bilangan yang didalam kurung adalah bilangan yang habis dibagi 3 dan tidak habis dibagi 4.
Bilangan yang habis dibagi 3 dan habis dibagi 4 membentuk deret aritmatika berikut
12 + 24 + 36 + ... + 84 + 96
Misal
Jumlah bilangan Asli dari 10 sampai 99 yang habis dibagi 3 dan tidak habis dibagi 4 = S
Jumlah Bilangan Asli dari 10 sampai 99 yang habis dibagi 3 = Sx
Jumlah bilangan Asli dari 10 sampai 99 yang habus dibagi 3 dan habis dibagi 4 = Sy
Maka
Jumlah bilangan Asli dari 10 sampai 99 yang habis dibagi 3 dan tidak habis dibagi 4 = Jumlah Bilangan Asli dari 10 sampai 99 yang habis dibagi 3 = Sx - Jumlah bilangan Asli dari 10 sampai 99 yang habus dibagi 3 dan habis dibagi 4 = Sy
S = Sx - Sy
Untuk deret aritmatika Sx
12 + (15 + 18 + 21) + 24 + (27 + 30 + 33) + 36 + ... 84 + (87 + 90 + 93) + 96 + ( 99)
Diketahi a = 12, b = 15 - 12 = 3 dan Un = 99
Ambil Un = 99
Un = 99
a + (n - 1)b = 99
12 + (n - 1)3 = 99
(n - 1)3 = 99 - 12
(n - 1)3 = 87
n - 1 = 87/3
n - 1 = 29
n = 29 + 1 = 30
Karena n = 30 maka U30 = 99 dan akan dicari S30
Maka Sx = 1.665
Untuk deret aritmatika Sy
12 + 24 + 36 + ... + 84 + 96
Dik : a = 12, b = 24 - 12 = 12 dan Un = 96
Ambil Un = 96
Un = 96
a + (n - 1)b = 96
12 + (n - 1)12 = 96
(n - 1)12 = 96 - 12
(n - 1)12 = 84
n - 1 = 84/12
n - 1 = 7
n = 7 + 1 = 8
Karena n = 8 mak U8 = 96 dan akan dicari S8
Maka Sy = 432
Jadi
S = Sx - Sy
= 1.665 - 432 = 1.233
Kunci Jawaban : D
14. Diketahui barisan aritmatika -8, -5, -2, ..., 73 Tentukan banyak suku barisan tersebut
Pembahasan
Dik : a = -8
b = -5 - (-8) = -5 + 8 = 3
Un = 73
Dit : n = ....?
Un = a + (n - 1)b
73 = -8 + (n - 1) 3
73 = -8 + 3n - 3
73 = -11 + 3n
3n = 73 + 11
3n = 84
n = 84/3
n = 28
Jadi banyak suku dari barisan tersebut adalah 28
15. Diketahui barisan aritmarika dengan hasil penjumlahan suku ke-3 dan suku ke-5 adalah 68 dan hasil penjumlahan suku ke-6 dan suku ke-8 adalah 44. Tentukan suku ke-28 barisan tersebut.
Pembahasan
Dik : U3 + U5 = 68
U6 + U8 = 44
Dit : U28 = ....?
Jawab
U3 + U5 = 68
(a + 2b) + (a + 4b) = 68
2a + 6b = 68 (kedua ruas sama-sama dibagi 2)
a + 3b = 34 ......... (1)
U6 + U8 = 44
(a + 5b) + (a + 7b) = 44
2a + 12b = 44 (kedua ruas sama-sama dibagi 2)
a + 6b = 22 ........... (2)
Eliminasi a dari persamaan (1) dan (2)
Subtitusi b = -4 ke persamaan (1)
a + 3b = 34
a + 3(-4) = 34
a - 12 = 34
a = 34 + 12
a = 46
Sehingga diperoleh
U28 = a + 27b
= 46 + 27(-4)
= 46 - 108
= -62
Jadi besar suku ke-28 adalah -62
16. Diketahui barisan aritmatika dengan suku ke-2 adalah 17. Jika hasil penjumlahan suku ke-5, suku ke-7, dan suku ke-10 adalah -13. Tentukan beda barisan dan suku ke-6 barisan tersebut
Pembahasan
Dik : U2 = 17
U5 + U7 + U10 = -13
Dit : b = ....? dan
U6 = .....?
Jawab
U2 = 17
a + b = 17 ........ (1)
U5 + U7 + U10 = -13
(a + 4b) + (a + 6b) + (a + 9b) = -13
3a + 19 b = -13 ........ (2)
Eliminasi a dari persamaan (1) dan (2)
Jadi beda dari barisan tersebut adalah -4
Subtitusi b = -4 ke persamaan (1)
a + b = 17
a - 4 = 17
a = 17 + 4
a = 21
Sehingga diperoleh :
U6 = a + 5b
= 21 + 5(-4)
= 21 - 20
= 1
Jadi besar suku ke-6 adalah 1
17. Diketahui tiga bilangan membentuk barisan aritmatika dengan jumlah ketiga bilangan tersebut 33. Jika hasil kali ketiga bilangan tersenut 1.155. Tentukan ketiga bilangan tersebut.
Pembahasan
Misal ketiga bilangan yang membentuk barisan aritmatika adalah a, a+b, a+2b
Dik : a + (a + b) + (a + 2b) = 33
a(a+b)(a+2b) = 1.155
Dit: U1 = a = ....?
U2 = a+b = ....?
U3 = a + 2b = ....?
Jawab
a + (a + b) + (a + 2b) = 33
3a + 3b = 33
a + b = 11 .....(1)
a(a+b)(a+2b) = 1.155
a(a + b)(a+b +b) = 1.155
a(11)(11+b) = 1.155
a(11 + b) =105
dari persamaan (1) diperoleh
a = 11 - b
maka diperoleh
a(11 + b) =105
(11 - b)(11 + b) = 105
*) Untuk b = 4
Substitusi b = 4 ke persamaan (1)
a + b = 11
a + 4 = 11
a = 11 - 4
a = 7
U2 = a + b
= 7 + 4
= 11
U3 = a + 2b
= 7 + 2(4)
= 7 + 8
= 15
Jadi ketiga bilangan tersebut adalah 7, 11, 15
**) Untuk b = -4
a + b = 11
a - 4 = 11
a = 11 + 4
a = 15
U2 = a + b
= 15 - 4
= 11
U3 = a + 2b
= 15 + 2 (-4)
= 15 - 8= 7
Jadi ketiga bilangan tersebut adalah 15, 11, 7
Jadi ketiga bilangan tersbut adalah 7, 11, 15 dan 15, 11, 7
18. Diketahui barisan aritmatika dengan suku ke-n adalah Un. jika U3 = 23 dan U7 = 39, tentukan suku ke-29 barisan tersebut.
Pembahasan
Dik: U3 = 23, U7 = 39
Dit : U29 = ....?
Jawab
(Cara lain menentukan beda ini dapat dipelajari di link https://www.sambimatika.my.id/2021/10/barisan-dan-deret-aritmatika-materi-dan.html pada bagian pembahasan contoh 4.)
Subtitusi b = 4 ke U3 = 23
U3 = 23
a + 2b = 23
a + 2(4) = 23
a + 8 = 23
a = 23 - 8
a = 15
Sehingga diperoleh
U29 = a + 28b
= 15 + 28(4)
= 15 + 112
= 127
19. Suku tengah suatu barisan aritmatika adalah 249 dan suku terakhirnya 492. Jika suku ke-7 adalah 73, tentukan suku pertama, beda dan banyak suku barisan tersebut.
Pembahasan
Untuk menjawab soal diatas perhatikan terlebih dahulu ilustrasi berikut.
 |
| Gambar 1. Ilustrasi Suku Tengah Barisan Aritmatika |
Perhatikan pula ilustrasi berikut
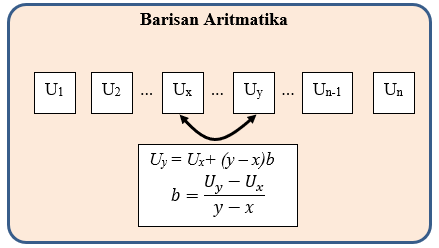 |
| Gambar 2. Beda suku barisan aritmatika yang tidak berurutan |
Berdasarkan ilustrasi diatas barisan aritmatika yang ditanyakan banyak sukunya haruslah ganjil sehingga
Diketahui :
Suku tengah = Suku ke 1/2(n + 1) dengan n ganjil
Un = 491
U7 = 73
Misal adalah beda yang dicari dari suku ke-7 dan suku tengah dan
adalah beda yang dicari dari suku tengah dan suku terakhir, maka diperoleh
dan
Karena barisan aritmatika maka =
sehingga diperoleh
=
Sehingga diperoleh banyak suku dari barisan aritmatika diatas adalah 45, maka
Subtitusi n = 45 ke atau
., Misal ke
Jadi beda barisan aritmatika tersebut adalah b = 11
dari U7 = 73 diperoleh
U7 = 73
a + 6b = 73
a + 6(11) = 73
a + 66 = 73
a = 73 - 66
a = 7
Jadi diperoleh a = 7, b = 11 dan n = 45
20. Antara bilangan 440 dan 1.256 disisipkan 15 bilangan sehingga membentuk barisan aritmatika. Tentukan beda dan suku ke-11 barisan tersebut.
Pembahasan
Dik barisan aritmatik 440, 1.256 sehingga diperoleh
U1 = a = 440
U2 = Un = 1.256
Dit : b = ....? dan U11 = ....?
Jika diantara bilangan tersebut disisipkan 15 bilangan sehingga membentuk barisan aritmatika, maka diperoleh barisan aritmatika baru. Perhatikan ilustrasi berikut
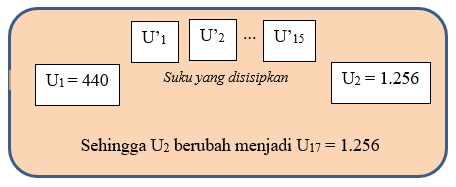 |
| Gambar 3. Sisipan suku pada barisan aritmatika |
Sehingga dari barisan aritmatika yang baru diperoleh :
U1 = a = 440 dan U17 = 1.256, maka
Sehingga
U11 = a + 10b
= 44 + 10(51)
= 44 + 510
= 950
Jadi Barisan aritmatika baru memiliki b = 51 dan U11 = 950
21. Diketahui barisan aritmatika 4, 16, 28, 40, ... , 160. Jika diantara dua suku berurutan disisipkan 3 bilangan sehingga terjadi barisan aritmatika baru, tentukan
a. Beda barisan baru setelah disisipkan dan
b. Suku ke-35 dari barisan baru setelah disisipkan
Pembahasan
Barisan aritmatika awal 4, 16, 28. 40, ... , 160
dari barisan awal diketahui a = 4, U2 = 16
Bentuk barisan aritmatika baru setelah disisipan tiga bilangan adalah
4, ...., ...., ...., 16, ...., ...., ...., 28, ...., ...., ...., 40, ... , 160
dari barisan baru diketahui
U1 = a = 4
U5 = 16
sehingga diperoleh
Maka
U35 = a + 34b
= 4 + 34(3)
= 4 + 102
= 106
Jadi dari barisan aritmatika baru diperoleh :
a. Beda baru, b = 3
b. U35 = 106
Demikian pembahasan Soal Barisan dan Deret Aritmatika Kelas X Fase E SMA/MA Kurikulum Merdeka, tulisan ini akan terus diupdate untuk memberikan sumber belajar tambahan untuk yang lagi mempelajari barisan deret aritmatika. Semoga bermanfaat.


Post a Comment
Terimakasih untuk anda telah berkomentar di postingan ini