Rasio Trigonometri dan Pembahasan Soal

Apa itu trigonometri ?

Secara etimologi, trigonometri berasal dari kata “trigonon” yang artinya tiga sudut, dan “metron” (mengukur). Jadi kalau bicara tentang trigonometri berarti bicara terkait dengan ukuran dan sudut.

Awal trigonometri dapat dilacak hingga zaman Mesir Kuno dan Babilonia dan peradaban Lembah Indus, lebih dari 3000 tahun yang lalu. Matematikawan India adalah perintis penghitungan variabel aljabar yang digunakan untuk menghitung astronomi dan juga trigonometri. Lagadha adalah matematikawan yang dikenal sampai sekarang yang menggunakan geometri dan trigonometri untuk penghitungan astronomi dalam bukunya Vedanga, Jyotisha, yang sebagian besar hasil kerjanya hancur oleh penjajah India.

Pada abad ke-12, trigonometri mulai dipelajari oleh Nashirudin at-Tusi sebagai ilmu yang lepas dari astronomi dan lebih merupakan ilmu yang berkaitan dengan segitiga, khususnya segitiga siku-siku.

Perbandingan Trigonometri

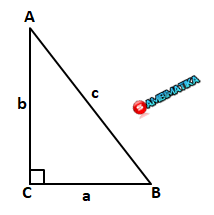
Perhatikan segitiga siku-siku berikut.

Ada enam perbandingan sisi-sisi segitiga siku-siku yaitu :

1. $https://latex.codecogs.com/svg.image?\frac{a}{b}$ dan $https://latex.codecogs.com/svg.image?\frac{b}{a}$

2. $https://latex.codecogs.com/svg.image?\frac{a}{c}$ dan $https://latex.codecogs.com/svg.image?\frac{c}{a}$

3. $https://latex.codecogs.com/svg.image?\frac{b}{c}$ dan $https://latex.codecogs.com/svg.image?\frac{c}{b}$

Relasi besar sudut dengan perbandingan sisi

Ada relasi yang menarik antara besar sudut dengan perbandingan sisi-sisi pada suatu segitiga siku-siku. Sebagai misal, relasi antara besar sudut A dengan perbandingan sisi $https://latex.codecogs.com/svg.image?\frac{a}{c}$ . Perhatikan bahwa jika besar sudut A berubah maka perbandingan $https://latex.codecogs.com/svg.image?\frac{a}{c}$ juga berubah. Dalam hal ini, dapat dilihat bahwa bila besar sudut A semakin besar maka perbandingan $https://latex.codecogs.com/svg.image?\frac{a}{c}$ juga semakin besar.

Lebih lanjut, dapat dipastikan bahwa tidak mungkin teerdapat dua sudut A yang berbeda yang berakibat perbandingannya $https://latex.codecogs.com/svg.image?\frac{a}{c}$ sama. Sifat-sifat ini menyatakan ada relasi fungsional antara besar sudut A dengan perbandingan $https://latex.codecogs.com/svg.image?\frac{a}{c}$ . Selanjutnya di dalam matematika, relasi fungsional tersebut disebut SINUS, dan disimbolkan dengan “sin”.

Berikut cara menulis relasi sinus tersebut:

$https://latex.codecogs.com/svg.image?\sin A=\frac{a}{c}$

Dibaca: “sinus A sama dengan a per c”.

Dapat ditunjukkan bahwa relasi besar sudut lainnya dengan perbandingan sisi yang manapun merupakan Fungsi.

Fungsi trigonometri dari perbandingan sisi segitiga siku-siku

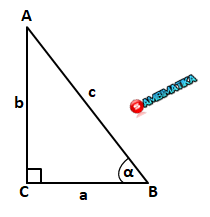
Perhatikan segitiga siku-siku ABC berikut

Dimisalkan besar sudut A adalah $https://latex.codecogs.com/svg.image?\alpha$ (dengan satuan derajat maupun radian), maka diperoleh

$https://latex.codecogs.com/svg.image?\sin \alpha =\frac{\mathrm{sisi\, depan\, sudut}}{\mathrm{sisi\, miring}}=\frac{b}{c}$

$https://latex.codecogs.com/svg.image?\cos \alpha =\frac{\mathrm{sisi\, samping\, sudut}}{\mathrm{sisi\, miring}}=\frac{a}{c}$

$https://latex.codecogs.com/svg.image?\tan \alpha =\frac{\mathrm{sisi\, depan\, sudut}}{\mathrm{sisi\, samping\, sudut}}=\frac{b}{a}$

$https://latex.codecogs.com/svg.image?\cot \alpha =\frac{\mathrm{sisi\, samping\, sudut}}{\mathrm{sisi\, depan\, sudut}}=\frac{a}{b}$

$https://latex.codecogs.com/svg.image?\sec \alpha =\frac{1}{\cos \alpha }=\frac{\mathrm{sisi\, miring}}{\mathrm{sisi\, samping\, sudut}}=\frac{c}{a}$

$https://latex.codecogs.com/svg.image?\csc \alpha =\frac{1}{\sin \alpha }=\frac{\mathrm{sisi\, miring}}{\mathrm{sisi\, depan\, sudut}}=\frac{c}{b}$

Sudut depresi dan sudut elevasi

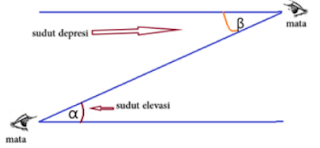
Dalam kehidupan sehari-hari, kita sering mendengar istilah “sudut elevasi” dan “sudut depresi”. Sudut elevasi adalah sudut yang dibentuk oleh horisontal dengan arah pandangan mata pengamat ke arah atas. Sedangkan sudut elevasi adalah sudut yang dibentuk oleh arah horizontal dengan arah pandangan mata ke arah bawah. Untuk lebih jelasnya, perhatikan gambar berikut ini.

Masalah kontekstual

Banyak sekali kita jumpai berbagai hal yang terkait dengan rasio trigonometri. Rasio trigonometri dapat digunakan untuk memecahkan masalah kontekstual yang berhubungan dengan sudut pengamatan, tinggi suatu benda , atau untuk menentukan jarak ke suatu obyek. Rasio trigonometri merupakan salah satu sarana yang dapat digunakan untuk melatih penalaran dalam menyelesaikan permasalahan tersebut.

Beberapa keterampilan yang perlu dimiliki untuk meningkatkan kemampuan memecahkan masalah adalah:

1. Memahami soal

Pahami soal atau masalah yang diberikan, kemudian tentukan beberapa hal berikut.

a. Menyatakan soal ke dalam bahasa sendiri

b. Membuat diagram dari soal tersebut

c. Menentukan apa fakta atau informasi yang diberikan

d. Menentukan apa yang ditanyakan, apa yang diminta untuk dicari atau dibuktikan

2. Memilih pendekatan atau strategi pemecahan

Setelah memahami soal, tentukanlah beberapa hal berikut.

a. Memilih dan menggunakan pengetahuan aljabar yang diketahui

b. Menentukan konsep yang relevan

c. Menentukan atau memilih variabel yang terlibat

d. Merumuskan model matematika atau kalimat matematika dari masalah

3. Menyelesaikan model

Setelah memilih strategi penyelesaian, tentukanlah beberapa hal berikut.

a. Tentukan jenis model matematikanya

b. Lakukan operasi hitung atau operasi aljabar secara benar untuk mendapatkan solusi dari permasalahan yang diberikan

4. Menafsirkan solusi

Setelah solusi atau penyelesaian dari model matematika diperoleh, selanjutnya lakukan hal berikut ini.

a. Periksalalah kelayakan atau kebenaran jawaban atau masuk akalnya jawaban

b. Solusi dari penyelesaian model matematika diterjemahkan ke dalam penyelesaian dari masalah semula

Contoh dan pembahasan soal

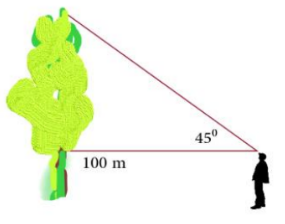
1. Sebuah pohon berjarak 100 meter dari seorang pengamat yang tingginya 170 cm. Apabila pucuk pohon tersebut dilihat pengamat dengan sudut elevasi $https://latex.codecogs.com/svg.image?60^{o}$ , tentukanlah tinggi pohon tersebut.

Penyelesaian

1. Memahami soal

Dari soal dapat dibuatkan diagramnya sebagai berikut.

Dari soal diketahui

Jarak pohon dengan pengamat = 100 m

Tingi pengamat = 170 cm = 1,7 m

Sudut elevasi = $https://latex.codecogs.com/svg.image?60^{o}$

Ditanyakan : Tinggi pohon = .....?

2. Memilih pendekatan atau stategi penyelesaian masalah

Konsep yang relevan dari soal diatas adalah perbandingan trigonometri

Misal h = tinggi pohon - tinggi pengamat

S = jarak pohon dengan pengamat

maka diperoleh

$https://latex.codecogs.com/svg.image?\tan 60^{o}=\frac{h}{S}$

3. Menyelesaikan model

Dengan menggunakan operasi hitung, diperoleh :

$https://latex.codecogs.com/svg.image?\tan 60^{o}=\frac{h}{S}$

$https://latex.codecogs.com/svg.image?\sqrt{3}=\frac{h}{100}$

$https://latex.codecogs.com/svg.image?h=100\sqrt{3}$

4. Menafsirkan solusi

Tinggi pohon = h + tinggi pengamat

$https://latex.codecogs.com/svg.image?=100\sqrt{3}+1,7$ m

Jadi tinggi pohon adalah $https://latex.codecogs.com/svg.image?100\sqrt{3}+1,7$ m.

2. Pada sebuah segitiga siku-siku diketahui $https://latex.codecogs.com/svg.image?\sin \alpha =a$ , maka nilai $https://latex.codecogs.com/svg.image?\tan \alpha=....$ (Soal UN Tahun 2018)

A. $https://latex.codecogs.com/svg.image?-\frac{a}{\sqrt{a^{2}-1}}$

B. $https://latex.codecogs.com/svg.image?-\frac{1}{\sqrt{a^{2}-1}}$

C. $https://latex.codecogs.com/svg.image?\frac{a}{\sqrt{a^{2}-1}}$

D. $https://latex.codecogs.com/svg.image?\frac{a}{\sqrt{1-a^{2}}}$

E. $https://latex.codecogs.com/svg.image?\frac{1}{\sqrt{1+a^{2}}}$

Pembahasan

Ingat bahwa

$https://latex.codecogs.com/svg.image?\sin \alpha =\frac{\mathrm{sisi\, depan\, sudut}}{\mathrm{sisi\, miring}}$

karena $https://latex.codecogs.com/svg.image?\sin \alpha =a$ maka sudah pasti sisi depan sudut = a dan sisi miring = 1 dan jika digambarkan segitiga siku-sikunya seperti pada gambar berikut

Untuk mencari panjang sisi samping sudut gunakanlah teorema pythagoras yaitu

Panjang sisi samping sudut $https://latex.codecogs.com/svg.image?=\sqrt{1^{2}-a^{2}}=\sqrt{1-a^{2}}$

Sehingga diperoleh

$https://latex.codecogs.com/svg.image?\tan \alpha =\frac{\mathrm{sisi\, depan\, sudut}}{\mathrm{sisi\, samping\, sudut}}$

$https://latex.codecogs.com/svg.image?=\frac{a}{\sqrt{1-a^{2}}}$

Kunci jawaban : D

3. Bagus berdiri dengan jarak 80 m dari sebuah menara memandang puncak menara dengan sudut elevasi $https://latex.codecogs.com/svg.image?30^{o}$ . Jika jarak mata Siti dengan tanah adalah 150 cm, tinggi menara tersebut adalah ... (Ujian Nasional Tahun 2018)

A. $https://latex.codecogs.com/svg.image?\left ( \frac{80}{3}\sqrt{3}+1,5 \right )$ m

B. $https://latex.codecogs.com/svg.image?\left ( \frac{80}{3}\sqrt{3}-1,5 \right )$ m

C. $https://latex.codecogs.com/svg.image?\left ( 80\sqrt{3}-1,5 \right )$ m

D. $https://latex.codecogs.com/svg.image?\left ( 80\sqrt{3}+1,5 \right )$ m

E. $https://latex.codecogs.com/svg.image?\left ( \frac{81,5}{3}\sqrt{3} \right )$ m

Pembahasan

Permasalahan diatas dapat diilustrasikan seperti gambar berikut

Misal h = tinggi menara - jarak mata bagus dengan tanah

x = jarak Siti dengan menara

t = tinggi menara

dengan menggunakan perbandingan trigonometri diperoleh

$https://latex.codecogs.com/svg.image?\tan \alpha =\frac{h}{x}$

$https://latex.codecogs.com/svg.image?\tan 30^{o} =\frac{h}{80}$

$https://latex.codecogs.com/svg.image?\frac{1}{3}\sqrt{3}=\frac{h}{80}$

$https://latex.codecogs.com/svg.image?h=\frac{80}{3}\sqrt{3}$

Tinggi menara = h + jarak mata bagus dengan tanah

$https://latex.codecogs.com/svg.image?t=\frac{80}{3}\sqrt{3}+1,5$

Jadi tinggi menara adalah $https://latex.codecogs.com/svg.image?t=\frac{80}{3}\sqrt{3}+1,5$ meter

Kunci jawaban : A

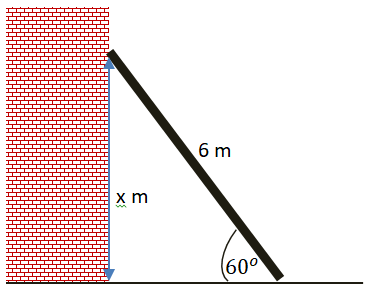
4. Sebuah tangga memiliki panjang 6 m. Tangga tersebut disandarkan pada tembok rumah dengan membentuk sudut $https://latex.codecogs.com/svg.image?60^{o}$ terhadap tanah. Ketinggian tembok yang dapat dicapai oleh ujung tangga dari permukaan tanah adalah ... (UNBK Tahun 2018)

A. $https://latex.codecogs.com/svg.image?2\sqrt{2}$ m

B. $https://latex.codecogs.com/svg.image?3\sqrt{2}$ m

C. $https://latex.codecogs.com/svg.image?2\sqrt{3}$ m

D. $https://latex.codecogs.com/svg.image?3\sqrt{3}$ m

E. $https://latex.codecogs.com/svg.image?6\sqrt{3}$ m

Pembahasan

Ilustrasi dari permasalahan diatas adalah seperti gambar berikut

Dari gambar diatas, perbandingan trigonometri yang tepat adalah sin, sehingga diperoleh :

Misal tinggi tembok yang mungkin = x, maka

$https://latex.codecogs.com/svg.image?\sin 60^{o}=\frac{x}{6}$

$https://latex.codecogs.com/svg.image?\frac{1}{2}\sqrt{3}=\frac{x}{6}$

$https://latex.codecogs.com/svg.image?x=6.\frac{1}{2}\sqrt{3}=3\sqrt{3}$

Jadi tinggi tembok yang mungkin yang dapat dicapai ujuang tangga dari permukaan tanah adalah $https://latex.codecogs.com/svg.image?3\sqrt{3}$ meter

Kunci jawaban : D

5. Diketahui segitiga ABC siku-siku di B dan sin A = $https://latex.codecogs.com/svg.image?\frac{12}{13}$ . Nilai sin C adalah ...

A. $https://latex.codecogs.com/svg.image?\frac{5}{12}$

B. $https://latex.codecogs.com/svg.image?\frac{5}{13}$

C. $https://latex.codecogs.com/svg.image?\frac{8}{12}$

D. $https://latex.codecogs.com/svg.image?\frac{7}{13}$

E. $https://latex.codecogs.com/svg.image?\frac{12}{13}$

Pembahasan

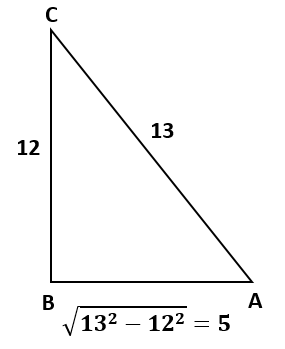
$https://latex.codecogs.com/svg.image?\sin A=\frac{\mathrm{sisi\, depan\, sudut}}{\mathrm{sisi\, miring}}$

$https://latex.codecogs.com/svg.image?\sin A=\frac{12}{13}$

Artinya bahwa panjang sisi depan sudut A adalah 12 dan panjang sisi miringnya 13, jika digambarkan segitiga siku-sikunya seperti gambar berikut

Dari gambar diketahui panjang AC = 13, BC = 12. Dengan menggunakan teorema pythagoras kita bisa mencari panjang AB = 5, sehingga kita bisa mencari nilai sin C yaitu

$https://latex.codecogs.com/svg.image?\sin C=\frac{\mathrm{sisi\, depan\, sudut}}{\mathrm{sisi\, miring}}$

$https://latex.codecogs.com/svg.image?\sin C=\frac{5}{13}$

Kunci jawaban : B

6. Sebuah tangga menyandar pada dinding dengan kemiringan $https://latex.codecogs.com/svg.image?60^{o}$ . Jika panjang tangga 5 meter, jarak dari kaki tangga ke dinding adalah ....

A. $https://latex.codecogs.com/svg.image?\frac{5}{2}$ meter

B. $https://latex.codecogs.com/svg.image?\frac{5}{2}\sqrt{2}$ meter

C. $https://latex.codecogs.com/svg.image?\frac{5}{2}\sqrt{3}$ meter

D. $https://latex.codecogs.com/svg.image?5\sqrt{2}$ meter

E. $https://latex.codecogs.com/svg.image?5\sqrt{3}$ meter

Pembahasan

Permasalahan pada soal dapat diilustrasikan dengan gambar berikut

Ditanyakan jarak kaki tangga ke dinding atau panjang y dari gambar diatas. Konsep yang tepat untuk menghitung nilai y adalah dengan cos, sehingga diperoleh :

$https://latex.codecogs.com/svg.image?\cos \alpha =\frac{\mathrm{sisi\, samping\, sudut}}{\mathrm{sisi\, miring}}$

$https://latex.codecogs.com/svg.image?\cos 60^{o}=\frac{y}{5}$

$https://latex.codecogs.com/svg.image?\frac{1}{2}=\frac{y}{5}$

$https://latex.codecogs.com/svg.image?y=\frac{5}{2}$

Jadi jawak kaki tanggal ke dinding adalah $https://latex.codecogs.com/svg.image?\frac{5}{2}$ meter

Kunci jawaban : A

7. Sisno diminta mengukur tinggi tiang bendera menggunakan klinometer. Saat pertama berdiri dengan melihat ujung tiang bendera, terlihat pada klinometer menunjuk pada sudut $https://latex.codecogs.com/svg.image?60^{o}$ . Kemudian ia bergerak menjauhi tiang bendera sejauh 10 meter dan terlihat pada klinometer sudut $https://latex.codecogs.com/svg.image?45^{o}$ . Tinggi tiang bendera adalah ....

A. $https://latex.codecogs.com/svg.image?\left ( 15+10\sqrt{3} \right )$ m

B. $https://latex.codecogs.com/svg.image?\left ( 15+5\sqrt{3} \right )$ m

C. $https://latex.codecogs.com/svg.image?\left ( 15-5\sqrt{3} \right )$ m

D. $https://latex.codecogs.com/svg.image?\left ( 15-10\sqrt{3} \right )$ m

E. $https://latex.codecogs.com/svg.image?\left ( 5+10\sqrt{3} \right )$ m

Pembahasan

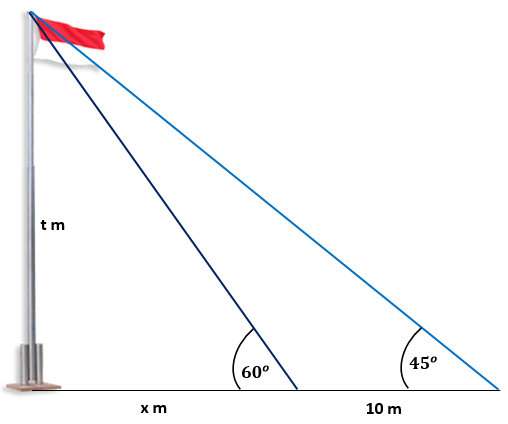
Soal diatas dapat diilustrasikan dengan gambar berikut.

Misal tinggi tiang bendera = t m

Jarak tiang bendera ke posisi pertama Sisno = x m

jarak tiang bendera ke posisi kedua Sisno = (10 + x) m

1. Dari posisi pertama Sisno diperoleh

$https://latex.codecogs.com/svg.image?\tan 60^{o}=\frac{t}{x}$

$https://latex.codecogs.com/svg.image?\sqrt{3}=\frac{t}{x}$

$https://latex.codecogs.com/svg.image?t=x\sqrt{3}$

2. Dari posisi kedua Sisno diperoleh

$https://latex.codecogs.com/svg.image?\tan 45^{o}=\frac{t}{10+x}$

$https://latex.codecogs.com/svg.image?1=\frac{t}{10+x}$

$t=10+x$

dari 1 dan 2 diperoleh

$https://latex.codecogs.com/svg.image?x\sqrt{3}=10+x$

$https://latex.codecogs.com/svg.image?x\sqrt{3}-x=10$

$https://latex.codecogs.com/svg.image?x\left ( \sqrt{3}-1 \right )=10$

$https://latex.codecogs.com/svg.image?x=\frac{10}{\sqrt{3}-1}$

subtitusi nilai x yang diperoleh persamaan 2

$t=10+x$

$https://latex.codecogs.com/svg.image?=10+\frac{10}{\sqrt{3}-1}$

$https://latex.codecogs.com/svg.image?=\frac{10\sqrt{3}}{\sqrt{3}-1}$

Rasionalkan penyebut

$https://latex.codecogs.com/svg.image?=\frac{10\sqrt{3}}{\sqrt{3}-1}.\frac{\sqrt{3}+1}{\sqrt{3}+1}$

$https://latex.codecogs.com/svg.image?=\frac{30+10\sqrt{3}}{2}$

$https://latex.codecogs.com/svg.image?=15+5\sqrt{3}$

Jadi tinggi tiang bendera adalah $https://latex.codecogs.com/svg.image?\left ( 15+5\sqrt{3} \right )$ meter

Kunci jawaban : B

8. Diketahui segitiga ABC siku-siku di B dan $https://latex.codecogs.com/svg.image?\sin R=\frac{8}{17}$ (P dan R sudut lancip). Nilai dari (1 - cos R)(1 + sin P) adalah ....

A. $https://latex.codecogs.com/svg.image?\frac{18}{7}$

B. $https://latex.codecogs.com/svg.image?\frac{17}{15}$

C. $https://latex.codecogs.com/svg.image?\frac{64}{289}$

D. $https://latex.codecogs.com/svg.image?-\frac{64}{249}$

E. $https://latex.codecogs.com/svg.image?-\frac{225}{249}$

Pembahasan

Perhatikan gambar segitiga siku-siku ABC berikut.

Karena $https://latex.codecogs.com/svg.image?\sin R=\frac{8}{17}$ , maka panjang AB = 8 dan AC = 17.

Dengan teorema pythagoras diperoleh panjang BC yaitu

$https://latex.codecogs.com/svg.image?BC=\sqrt{AC^{2}-AB^{2}}$

$https://latex.codecogs.com/svg.image?=\sqrt{17^{2}-8^{2}}$

$https://latex.codecogs.com/svg.image?=\sqrt{289-64}$

$https://latex.codecogs.com/svg.image?=\sqrt{225}=15$

Setelah itu dapat ditentukan nilai dari cos R dan sin P yaitu

$https://latex.codecogs.com/svg.image?\cos R=\frac{BC}{AC}=\frac{15}{17}$

$https://latex.codecogs.com/svg.image?\sin P=\frac{BC}{AC}=\frac{15}{17}$

Sehingga diperoleh nilai dari

$https://latex.codecogs.com/svg.image?\left (1-\cos R \right )\left ( 1+\sin P \right )=\left ( 1-\frac{15}{17} \right )\left ( 1+\frac{15}{17} \right )$

$https://latex.codecogs.com/svg.image?=1^{2}-\left ( \frac{15}{17} \right )^{2}$

$https://latex.codecogs.com/svg.image?=1-\frac{225}{289}$

$https://latex.codecogs.com/svg.image?=\frac{289-225}{289}$

$https://latex.codecogs.com/svg.image?=\frac{64}{289}$

Kunci jawaban : C

9. Diketahui segitiga ABC siku-siku di A dan $https://latex.codecogs.com/svg.image?\sin B=\frac{3}{7}$ , nilai tan C adalah ....

A. $https://latex.codecogs.com/svg.image?\frac{3}{7}\sqrt{10}$

B. $https://latex.codecogs.com/svg.image?\frac{7}{20}\sqrt{10}$

C. $https://latex.codecogs.com/svg.image?\frac{2}{3}\sqrt{10}$

D. $https://latex.codecogs.com/svg.image?\frac{3}{2}\sqrt{10}$

E. $https://latex.codecogs.com/svg.image?\frac{7}{3}\sqrt{10}$

Pembahasan

Perhatikan segitiga ABC sesuai dengan soal diatas berikut

Karena $https://latex.codecogs.com/svg.image?\sin B=\frac{3}{7}$ , maka panjang AC = 3 dan BC = 7. Untuk menentukan panjang AB digunakan teorema pythagoras yaitu :

$https://latex.codecogs.com/svg.image?AB=\sqrt{BC^{2}-AC^{2}}$

$https://latex.codecogs.com/svg.image?=\sqrt{7^{2}-3^{2}}$

$https://latex.codecogs.com/svg.image?=\sqrt{49-9}$

$https://latex.codecogs.com/svg.image?=\sqrt{40}$

$https://latex.codecogs.com/svg.image?=\sqrt{4.10}=2\sqrt{10}$

Selanjutnya kita dapat menghitung nilai dari tan C yaitu :

$https://latex.codecogs.com/svg.image?\tan C=\frac{AB}{AC}$

$https://latex.codecogs.com/svg.image?=\frac{2\sqrt{10}}{3}$

$https://latex.codecogs.com/svg.image?=\frac{2}{3}\sqrt{10}$

Kunci jawaban : C

10. Andi berada di titik A dan berjarak $https://latex.codecogs.com/svg.image?6\sqrt{3}$ m dari titik B dengan sudut elevasi di titik A terhadap puncak tiang bendera adalah $https://latex.codecogs.com/svg.image?60^{o}$ . Andi ingin memasang tali dengan cara merobohkan tiang bendera. Dia harus bergerak menuju titik C sehingga jarak antara tiang bendera ke titik C adalah 2 m seperti gambar berikut.

Jika $https://latex.codecogs.com/svg.image?\alpha$ adalah sudut yang dibentuk BP' dan BC, maka nilai $https://latex.codecogs.com/svg.image?\frac{1}{\sin \alpha }$ adalah ......

Pembahasan

Diketahui : sudut elevasi di titik A = $https://latex.codecogs.com/svg.image?60^{o}$

AB = $https://latex.codecogs.com/svg.image?6\sqrt{3}$ m

CP' = 2 m

BP = BP'

Ditanyakan : $https://latex.codecogs.com/svg.image?\frac{1}{\sin \alpha }$

Perhatikan segitiga ABP

$https://latex.codecogs.com/svg.image?\tan A=\frac{BP}{AB}$

$https://latex.codecogs.com/svg.image?\tan 60^{o}=\frac{BP}{6\sqrt{3}}$

$https://latex.codecogs.com/svg.image?\sqrt{3}=\frac{BP}{6\sqrt{3}}$

$BP=18$

Karena BP = BP' maka BP' = 18

Perhatikan segitiga BCP'

Sudut CBP' = $https://latex.codecogs.com/svg.image?\alpha$ , maka

$https://latex.codecogs.com/svg.image?\frac{1}{\sin \alpha }=\frac{1}{\frac{CP'}{BP'}}$

$https://latex.codecogs.com/svg.image?=\frac{BP'}{CP'}$

$https://latex.codecogs.com/svg.image?=\frac{8}{2}=4$

Selanjutnya bisa mempelajari penyelesaian dari persamaan persamaan trigonometri melalui link https://s.id/persamaan_trigonometri atau bisa scan kode QR berikut

Menurut hemat penulis kiranya bisa mencoba cara menentukan nilai sinus, cosinus, tan dan lainnya tanpa menggunakan kalkulator atau tabel. Selengkapnya dapat dibaca melalui link https://www.sambimatika.my.id/2022/10/cara-menentukan-nilai-sin-cos-tan-tanpa.html

Selamat mencoba, tetap semangat dan semoga kesuksesan selalu menyertai kita semua. Amiin.

Demikian pembahasan rasio trigonometri dan pembahasan soal, semoga bermanfaat.

Rasio Trigonometri dan Pembahasan Soal

Apa itu trigonometri ?

Perbandingan Trigonometri

Relasi besar sudut dengan perbandingan sisi

Fungsi trigonometri dari perbandingan sisi segitiga siku-siku

Sudut depresi dan sudut elevasi

Contoh dan pembahasan soal

Post a Comment

Post a Comment

Contact Form

Rasio Trigonometri dan Pembahasan Soal

Apa itu trigonometri ?

Perbandingan Trigonometri

Relasi besar sudut dengan perbandingan sisi

Fungsi trigonometri dari perbandingan sisi segitiga siku-siku

Sudut depresi dan sudut elevasi

Contoh dan pembahasan soal

You might like

Post a Comment

Post a Comment

Contact Form