Pertidaksamaan eksponen dan pembahasan soal

Apa itu pertidaksamaan eksponen ?

Pertidaksamaan eksponen adalah pertidaksamaan jenis eksponen yang memiliki variabel.

Sifat-sifat pada pertidaksamaan eksponen

Sifat-sifat yang berlaku pada pertidaksamaan eksponen adalah sebagai berikut

1. Jika a > 1 dan $https://latex.codecogs.com/svg.image?a^{f(x)}>a^{g(x)}$ maka f(x) > g(x)

2. jika a > 1 dan $https://latex.codecogs.com/svg.image?a^{f(x)}<a^{g(x)}$ maka f(x) < g(x)

3. Jika 0 < a < 1 dan $https://latex.codecogs.com/svg.image?a^{f(x)}>a^{g(x)}$ maka f(x) < g(x)

4. Jika 0 < a < 1 dan $https://latex.codecogs.com/svg.image?a^{f(x)}<a^{g(x)}$ maka f(x) > g(x)

Contoh soal dan pembahasan

Tentukan himpunan penyelesaian dari pertidaksamaan ekponen berikut

1. $https://latex.codecogs.com/svg.image?2^{2x-5}>16^{x-7}$

Pembahasan

$https://latex.codecogs.com/svg.image?2^{2x-5}>16^{x-7}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 2^{2x-5}>\left ( 2^{4} \right )^{x-7}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 2^{2x-5}>2^{4x-28}$

Perhatikan bahwa 2 > 1 maka berlaku f(x) > g(x), sehingga diperoleh

$https://latex.codecogs.com/svg.image?\Leftrightarrow 2x-5>4x-28$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 2x-4x>-28+5$

$https://latex.codecogs.com/svg.image?\Leftrightarrow -2x>-23$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 2x<23$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x<\frac{23}{2}$

Jadi himpunan penyelesaian ari pertidaksamaan eksponen diatas adalah $https://latex.codecogs.com/svg.image?\left\{x|x>\frac{23}{2} \right\}$

(Cermati perubahan tanda ketidaksamaan yang terjadi)

2. $https://latex.codecogs.com/svg.image?4^{\left ( x-4 \right )\left ( x+1 \right )}<\frac{1}{16}$

Pembahasan

$https://latex.codecogs.com/svg.image?4^{\left ( x-4 \right )\left ( x+1 \right )}<\frac{1}{16}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 4^{\left ( x-4 \right )\left ( x+1 \right )}<16^{-1}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 4^{\left ( x-4 \right )\left ( x+1 \right )}<4^{-2}$

Perhatikan bahwa 4 > 1 maka beraku f(x) < g(x) sehingga diperoleh

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( x-4 \right )\left ( x+1 \right )<-2$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x^{2}-3x-4<-2$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x^{2}-3x-2<0$

Untuk menyelesaikan masalah ini ingat kembali rumus ABC bisa dilihat DISINI

$https://latex.codecogs.com/svg.image?x_{1,2}=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}$

$https://latex.codecogs.com/svg.image?x_{1,2}=\frac{-\left ( -3 \right )\pm \sqrt{\left ( -3 \right )^{2}-4.1.(-2)}}{2.1}$

$https://latex.codecogs.com/svg.image?x_{1,2}=\frac{3\pm \sqrt{9+8}}{2}$

$https://latex.codecogs.com/svg.image?x_{1,2}=\frac{3\pm \sqrt{17}}{2}$

$https://latex.codecogs.com/svg.image?x_{1}=\frac{3+ \sqrt{17}}{2}$

$https://latex.codecogs.com/svg.image?x_{2}=\frac{3- \sqrt{17}}{2}$

Masukkan kedua nilai x tersebut ke garis bilangan

Dari garis bilangan tersebut terlihat bahwa nilai x yang memenuhi adalah $https://latex.codecogs.com/svg.image?\frac{3- \sqrt{17}}{2}<x< \frac{3+ \sqrt{17}}{2}$

Jadi himpunan penyelesaian ari pertidaksamaan eksponen diatas adalah $https://latex.codecogs.com/svg.image?\left\{x|\frac{3- \sqrt{17}}{2}<x< \frac{3+ \sqrt{17}}{2} \right\}$

3. $https://latex.codecogs.com/svg.image?\sqrt{\left ( \frac{1}{2} \right )^{2x+1}}>\left ( \frac{1}{4} \right )^{x-2}$

Pembahasan

$https://latex.codecogs.com/svg.image?\sqrt{\left ( \frac{1}{2} \right )^{2x+1}}>\left ( \frac{1}{4} \right )^{x-2}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( \frac{1}{2} \right )^{\frac{2x+1}{2}}>\left ( \frac{1}{2} \right )^{2x-4}$

Perhatikan bahwa $https://latex.codecogs.com/svg.image?0<\frac{1}{2}<1$ , maka f(x) < g(x) sehingga diperoleh

$https://latex.codecogs.com/svg.image?\Leftrightarrow \frac{2x+1}{2}<2x-4$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 2x+1<4x-8$

$https://latex.codecogs.com/svg.image?\Leftrightarrow -2x<-9$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 2x>9$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x>\frac{9}{2}$

Jadi himpunan penyelesaian ari pertidaksamaan eksponen diatas adalah $https://latex.codecogs.com/svg.image?\left\{x|x>\frac{9}{2} \right\}$

(Cermati perubahan tanda ketidaksamaan yang terjadi)

4. $https://latex.codecogs.com/svg.image?\left ( \frac{1}{3} \right )^{-x^{2}+2x+8}>\left ( \frac{1}{3} \right )^{x+2}$

Pembahasan

$https://latex.codecogs.com/svg.image?\left ( \frac{1}{3} \right )^{-x^{2}+2x+8}>\left ( \frac{1}{3} \right )^{x+2}$

Perhatikan bahwa $https://latex.codecogs.com/svg.image?0<\frac{1}{3}<1$ maka f(x) < g(x) sehingga diperoleh

$https://latex.codecogs.com/svg.image?\Leftrightarrow -x^{2}+2x+8<x+2$

$https://latex.codecogs.com/svg.image?\Leftrightarrow -x^{2}+x+6<0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x^{2}-x-6>0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( x-3 \right )\left ( x+2 \right )>0$

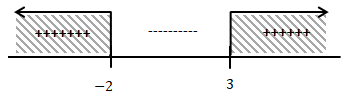
Pembuat nol fungsi

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( x-3 \right )\left ( x+2 \right )=0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x=3\, \, \mathrm{atau} \, \, x=-2$

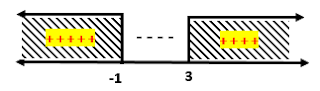
Masukkan nilai x yang diperoleh ke garis bilangan

Dari garis bilangan terlihat bahwa nilai x yang memenuhi adalah x < - 2 atau x > 3

Jadi himpunan penyelesaian ari pertidaksamaan eksponen diatas adalah {x| x < -2 atau x > 3}

5. $https://latex.codecogs.com/svg.image?\left ( \frac{1}{4} \right )^{3x+2}>\sqrt{\frac{8}{2^{x-2}}}$

Pembahasan

$https://latex.codecogs.com/svg.image?\left ( \frac{1}{4} \right )^{3x+2}>\sqrt{\frac{8}{2^{x-2}}}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( \frac{1}{4} \right )^{3x+2}>\left ( \frac{8}{2^{x-2}} \right )^{\frac{1}{2}}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( \frac{1}{2^{2}} \right )^{3x+2}>\left ( \frac{2^{3}}{2^{x-2}} \right )^{\frac{1}{2}}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( 2^{-2} \right )^{3x+2}>\left ( 2^{3-x+2}\right )^{\frac{1}{2}}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 2^{-6x-4}>2^{\frac{-x+5}{2}}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow -6x-4>\frac{-x+5}{2}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow -12x-8>-x+5$

$https://latex.codecogs.com/svg.image?\Leftrightarrow -11x>13$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 11x<-13$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x<-\frac{13}{11}$

Jadi himpunan penyelesaian ari pertidaksamaan eksponen diatas adalah $https://latex.codecogs.com/svg.image?\left\{x| x<-\frac{13}{11} \right\}$

6. $https://latex.codecogs.com/svg.image?5^{4x^{2}-6x-7}>5^{-5x-4}$

Pembahasan

$https://latex.codecogs.com/svg.image?5^{4x^{2}-6x-7}>5^{-5x-4}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 4x^{2}-6x-7>-5x-4$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 4x^{2}-x-3>0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( 4x+3 \right )\left ( x-1 \right )>0$

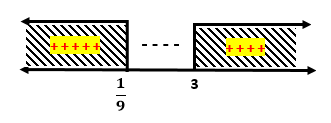
Pembuat nol fungsi

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( 4x+3 \right )\left ( x-1 \right )=0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x=-\frac{3}{4}\, \, \mathrm{atau}\, \, x=1$

Masukkan nilai x diatas ke garis bilangan

Pertidaksamaan eksponen dan pembahasan soal

Diperoleh nilai x yang memenuhi adalah $https://latex.codecogs.com/svg.image?x<-\frac{3}{4}\, \, \mathrm{atau}\, \, x>1$

Jadi himpunan penyelesaian dari pertidaksamaan eksponen diatas adalah $https://latex.codecogs.com/svg.image?\left\{x|x<-\frac{3}{4}\, \, \mathrm{atau}\, \, x>1 \right\}$

7. $https://latex.codecogs.com/svg.image?\sqrt{5^{2x+1}}<25^{x-2}$

Pembahasan

$https://latex.codecogs.com/svg.image?\sqrt{5^{2x+1}}<25^{x-2}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( 5^{2x+1} \right )^{\frac{1}{2}}<\left ( 5^{2} \right )^{x-2}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 5^{\frac{2x+1}{2}}<5^{2x-4}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \frac{2x+1}{2}<2x-4$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 2x+1<4x-8$

$https://latex.codecogs.com/svg.image?\Leftrightarrow -2x<-9$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 2x>9$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x>\frac{9}{2}$

Jadi himpunan penyelesaian dari pertidaksamaan eksponen diatas adalah $https://latex.codecogs.com/svg.image?\left\{x|x>\frac{9}{2} \right\}$

Baca Juga :

Persamaan logaritma

Fungsi logaritma

Pertidaksamaan logaritma dan pembahasan soal

Persamaan eksponen dan pembahasan soal

Fungsi eksponen

8. $https://latex.codecogs.com/svg.image?3^{2x+3}-84.3^{x}+9>0$

Pembahasan

$https://latex.codecogs.com/svg.image?3^{2x+3}-84.3^{x}+9>0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( 3^{x} \right )^{2}.3^{3}-84.3^{x}+9>0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 27\left ( 3^{x} \right )^{2}-84.3^{x}+9>0$

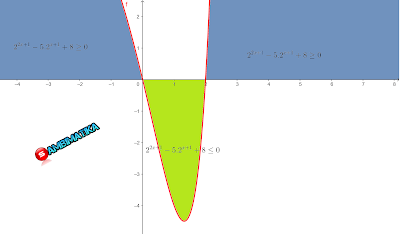
Misal $https://latex.codecogs.com/svg.image?y=3^{x}$ , diperoleh pertidaksamaan berikut

$https://latex.codecogs.com/svg.image?\Leftrightarrow 27y^{2}-84y+9>0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 9y^{2}-28y+3>0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( 9y-1 \right )\left ( y-3 \right )>0$

Pembuat nol fungsi

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( 9y-1 \right )\left ( y-3 \right )=0$

$https://latex.codecogs.com/svg.image?y=\frac{1}{9}\, \, \mathrm{atau} \, \, y=3$

Masukkan nilai y ke garis bilangan

Nilai y yang memenuhi adalah $https://latex.codecogs.com/svg.image?y<\frac{1}{9}\, \, \mathrm{atau}\, \, y>3$

Cek nilai y yang diperoleh ke permisalan

$https://latex.codecogs.com/svg.image?y<\frac{1}{9}\Leftrightarrow 3^{x}<\frac{1}{9}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 3^{x}<3^{-2}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x<-2$

atau

$https://latex.codecogs.com/svg.image?y>3\Leftrightarrow 3^{x}>3$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x>1$

Nilai x yang memenuhi adalah x < -2 atau x > 1

Jadi himpunan penyelesaian dari pertidaksamaan eksponen diatas adalah {x | x < -2 atau x > 1}

Baca Juga :

Persamaan eksponen

Fungsi eksponen

9. $https://latex.codecogs.com/svg.image?9^{x}+2.3^{x+1}>27$

Pembahasan

$https://latex.codecogs.com/svg.image?9^{x}+2.3^{x+1}>27$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( 3^{2} \right )^{x}+2.3^{x}.3-27>0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( 3^{x} \right )^{2}+6.3^{x}-27>0$

Misal $https://latex.codecogs.com/svg.image?y=3^{x}$ , diperoleh pertidakamaan berikut

$https://latex.codecogs.com/svg.image?\Leftrightarrow y^{2}+6y-27>0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( y+9 \right )\left ( y-3 \right )>0$

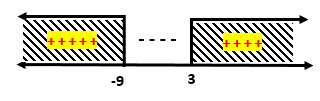
Pembuat nol fungsi

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( y+9 \right )\left ( y-3 \right )=0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow y=-9 \, \, \mathrm{atau}\, \, y=3$

Masukkan nilai y ke garis bilangan

Nilai y yang memenui adalah y < - 9 atau y > 3

Cek nilai y yang diperoleh ke permisalan

$https://latex.codecogs.com/svg.image?y<-9\Leftrightarrow 3^{x}<-9$

Perhatikan bahwa $https://latex.codecogs.com/svg.image?3^{x}$ selalu bernilai positif sehingga tidak ada nilai x yang memenuhi pertidaksamaan diatas

$https://latex.codecogs.com/svg.image?y>3\Leftrightarrow 3^{x}>3$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x>1$

Jadi himpunan penyelesaian dari pertidaksamaan eksponen diatas adalah {x | x > 1}

10. $https://latex.codecogs.com/svg.image?2^{2x+1}-5.2^{x+1}+8\geq 0$

Pembahasan

$https://latex.codecogs.com/svg.image?2^{2x+1}-5.2^{x+1}+8\geq 0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 2\left ( 2^{x} \right )^{2}-10.2^{x}+8\geq 0$

Misal $https://latex.codecogs.com/svg.image?y=2^{x}$ , diperoleh pertidaksamaan berikut

$https://latex.codecogs.com/svg.image?\Leftrightarrow 2y^{2}-10y+8\geq 0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow y^{2}-5y+4\geq 0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( y-1 \right )\left ( y-4 \right )\geq 0$

Pembuat nol fungsi

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( y-1 \right )\left ( y-4 \right )= 0$

$https://latex.codecogs.com/svg.image?y=1\, \, \mathrm{atau}\, \, y=4$

Masukkan nilai y ke garis bilangan

Nilai y yang memenuhi adalah $https://latex.codecogs.com/svg.image?y\leq 1\, \, \mathrm{atau}\, \, y\geq 4$

Cek nilai y yang diperoleh ke permisalan

$https://latex.codecogs.com/svg.image?y\leq 1\Leftrightarrow 2^{x}\leq 1\Leftrightarrow x\leq 0$

$https://latex.codecogs.com/svg.image?y\geq 4\Leftrightarrow 2^{x}\geq 4\Leftrightarrow x\geq 2$

Jadi himpunan penyelesaian dari pertidaksamaan eksponen diatas adalah $https://latex.codecogs.com/svg.image?\left\{x|x\leq 0\, \, \mathrm{atau}\, \, x\geq 2 \right\}$

11. $https://latex.codecogs.com/svg.image?\left ( 2x \right )^{1+^{2} \log 2x}>64x^{3}$

Pembahasan

$https://latex.codecogs.com/svg.image?\left ( 2x \right )^{1+^{2} \log 2x}>64x^{3}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 2x\left ( 2x \right )^{\, ^{2} \log 2x}>2^{3}\left ( 2x \right )^{3}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 2x\left ( 2x \right )^{\, ^{2} \log 2x}>8\left ( 2x \right )^{3}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( 2x \right )^{\, ^{2} \log 2x}>8\left ( 2x \right )^{2}$

Misal $https://latex.codecogs.com/svg.image?y=\, ^{2}\log 2x$ maka $https://latex.codecogs.com/svg.image?2^{y}=2x$ (Ingat bahwa $https://latex.codecogs.com/svg.image?a^{c}=b\Leftrightarrow \, ^{a}\log b=c$ ), sehingga diperoleh pertidaksamaan berikut

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( 2^{y} \right )^{y}>8\left ( 2^{y} \right )^{2}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 2^{y^{2}}>8. 2^{2y}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 2^{y^{2}}>2^{3}. 2^{2y}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 2^{y^{2}}>2^{2y+3}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow y^{2}>2y+3$

$https://latex.codecogs.com/svg.image?\Leftrightarrow y^{2}-2y-3>0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( y+1 \right )\left ( y-3 \right )>0$

Pembuat nol fungsi

$https://latex.codecogs.com/svg.image?\Leftrightarrow \left ( y+1 \right )\left ( y-3 \right )=0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow y=-1\, \, \mathrm{atau}\, \, y=3$

Masukkan nilai y ke garis bilangan

Nilai y yang memenuhi adalah y < -1 atau y > 3

Cek nilai y yang diperoleh ke permisalan

$https://latex.codecogs.com/svg.image?y<-1\Leftrightarrow \, ^{2}\log 2x <-1$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, ^{2}\log 2x <-^{2}\log 2$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, ^{2}\log 2x <^{2}\log 2^{-1}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, ^{2}\log 2x <^{2}\log \frac{1}{2}$

Karena a > 1 maka f(x) < g(x)

$https://latex.codecogs.com/svg.image?\Leftrightarrow 2x<\frac{1}{2}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x<\frac{1}{4}$

$https://latex.codecogs.com/svg.image?y>3\Leftrightarrow \, ^{2}\log 2x>3$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, ^{2}\log 2x>3\, ^{2}\log 2$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, ^{2}\log 2x>\, ^{2}\log 2^{3}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, ^{2}\log 2x>\, ^{2}\log 8$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, 2x>8$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, x>4$

Syarat agar $https://latex.codecogs.com/svg.image?\,^{2}\log 2x$ terdefinisi adalah

$https://latex.codecogs.com/svg.image?2x>0\Leftrightarrow x>0$

Masukkan semua nilai x yang diperoleh ke garis bilangan

Perhatikan yang paling banyak arsirannya adalah $https://latex.codecogs.com/svg.image?0<x<\frac{1}{4}\, \, \mathrm{atau}\, \, x>4$

Jadi himpunan penyelesaian dari pertidaksamaan eksponen diatas adalah $https://latex.codecogs.com/svg.image?\left\{x\, |\, 0<x<\frac{1}{4}\, \, \mathrm{atau}\, \, x>4 \right\}$

Demikian pembahasan tentang pertidaksamaan eksponen dan pembahasan soal, semoga bermanfaat.

Pertidaksamaan eksponen dan pembahasan soal

Apa itu pertidaksamaan eksponen ?

Sifat-sifat pada pertidaksamaan eksponen

Contoh soal dan pembahasan

Post a Comment

Post a Comment

Contact Form

Pertidaksamaan eksponen dan pembahasan soal

Apa itu pertidaksamaan eksponen ?

Sifat-sifat pada pertidaksamaan eksponen

Contoh soal dan pembahasan

You might like

Post a Comment

Post a Comment

Contact Form