Soal Anchor USBN Matematika Minat 2019 dan Pembahasannya

Apa itu soal anchor USBN ?

Soal anchor USBN adalah soal Ujian Sekolah Berstandar Nasional yang dibuat oleh pemerintah yang wajib ada di soal USBN yang dibuat oleh MGMP dan tidak boleh diubah redaksi soal dan nomor soalnya. Soal ini dimaksudkan sebagai standarisasi soal USBN dan yang dibuat oleh MGMP.

Berikut pembahasan soal anchor USBN matematika peminatan tahun 2019.

Soal Pilihan Ganda

3. Return adalah keuntungan dari suatu investasi. Sebagai contoh, jika investasi berupa tabungan di bank, return adalah bunga bank; jika investasi berupa kepemilikan saham pada suatu perusahaan, return dapat berupa kenaikan harga saham maupun bagi keuntungan perusahaan. Jika return yang diperoleh diinvestasikan kembali berlaku hubungan berikut :

$https://latex.codecogs.com/svg.image?1+R=(1+r)^{t}$

dengan R adalah return selama jangka waktu t, dan r adalah tingkat return per-unit waktu.

Ayah berinvestasi pada suatu perusahaan sebesar Rp 10.000.000,00 dengan return 15% pertahun. Saat pembagian keuntungan di tiap akhir tahun, Ayah menginvestasikan kembali keuntungan tersebut. Di akhir tahun ke-t, investasi Ayah di perusahaan tersebut bernilai Rp 15.200.000,00 (pembulatan ke ratusan ribu terdekat). Diketahui log 1,52 = 0,18 dan log 1,15 = 0,06. Nilai t adalah ....

A. 2

B. 3

C. 4

D. 5

E. 6

Pembahasan

Besar Investasi awal = Rp 10.000.000,00

Besar investasi di akhir tahun ke-t = Rp. 15.200.000,00

Keuntungan selama t tahun = 15.200.000 - 10.000.000 = 5.200.000

Persentase keuntungan (R) selama t tahun adalah

$https://latex.codecogs.com/svg.image?R=\frac{5.200.000}{10.000.000}x100%=52%$

Dari soal diketahui besar return per tahun (r) adalah

r = 15%

Untuk menentukan nilai t, substitusikan R dan r ke rumus pada soal diatas

$https://latex.codecogs.com/svg.image?1+R=(1+r)^{t}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 1+52%=(1+15%)^{t}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 1+0,52=(1+0,15)^{t}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 1,52=(1,15)^{t}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow t=\, \, ^{1,15}\log 1,52$

$https://latex.codecogs.com/svg.image?\Leftrightarrow t=\frac{\log 1,52}{\log 1,15}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow t=\frac{0,18}{0,06}=3$

Jadi nilai t adalah 3 tahun.

Kunci jawaban : B

5. Diketahui (x - 1) salah satu faktor dari persamaan suku banyak $https://latex.codecogs.com/svg.image?x^{3}-2x^{2}-5x+b=0$ . Salah satu faktor lainnya adalah ....

A. x - 3

B. x - 2

C. x + 4

D. x + 3

E. x + 6

Pembahasan

Cara 1

Akan digunakan cara pembagian bersusun yaitu

Dari pembagian diatas terlihat bahwa hasil baginya adalah $https://latex.codecogs.com/svg.image?x^{2}-x-6$ dengan sisa b - 6

Jika difaktorkan menjadi $https://latex.codecogs.com/svg.image?x^{2}-x-6=(x-3)(x+2)$

Sehingga faktor lain dari persamaan suku banyak diatas adalah (x - 3) atau (x + 2)

Cara 2

Menggunakan cara horner

Diperolah hasil baginya adalah $https://latex.codecogs.com/svg.image?x^{2}-x-6$ dengan sisa b - 6

Jika difaktorkan menjadi $https://latex.codecogs.com/svg.image?x^{2}-x-6=(x-3)(x+2)$

Sehingga faktor lain dari persamaan suku banyak diatas adalah (x - 3) atau (x + 2)

Kunci jawaban : A

10. Nilai $https://latex.codecogs.com/svg.image?\displaystyle \lim_{ x\to 0}\frac{\sin 8x+\sin 4x}{2x(\cos 12x+\cos 8x)}=....$

A. -3

B $https://latex.codecogs.com/svg.image?-\frac{3}{10}$

C. $https://latex.codecogs.com/svg.image?\frac{1}{5}$

D. $https://latex.codecogs.com/svg.image?\frac{3}{10}$

E. 3

Pembahasan

$https://latex.codecogs.com/svg.image?\displaystyle \lim_{ x\to 0}\frac{\sin 8x+\sin 4x}{2x(\cos 12x+\cos 8x)}$

$https://latex.codecogs.com/svg.image?=\displaystyle \lim_{ x\to 0}\frac{\sin 8x+\sin 4x}{2x}.\frac{1}{\cos 12x+\cos 8x}$

$https://latex.codecogs.com/svg.image?=\displaystyle \lim_{ x\to 0}\left ( \frac{\sin 8x}{2x}+\frac{\sin 4x}{2x} \right ).\displaystyle \lim_{x \to 0}\frac{1}{\cos 12x+\cos 8x}$

$https://latex.codecogs.com/svg.image?=(4+2).\frac{1}{\cos 0+\cos 0}$

$https://latex.codecogs.com/svg.image?=6.\frac{1}{2}=3$

Cara 2

Ingat bahwa

$https://latex.codecogs.com/svg.image?\sin A+\sin B=2\sin \frac{A+B}{2}\cos\frac{A-B}{2}$

$https://latex.codecogs.com/svg.image?\cos A+\cos B=2\cos \frac{A+B}{2}\cos\frac{A-B}{2}$

Sehingga diperoleh

$https://latex.codecogs.com/svg.image?\displaystyle \lim_{ x\to 0}\frac{\sin 8x+\sin 4x}{2x(\cos 12x+\cos 8x)}$

$https://latex.codecogs.com/svg.image?=\displaystyle \lim_{ x\to 0}\frac{2\sin 6x\cos 2x}{2x.2\cos 10x\cos 2x}$

$https://latex.codecogs.com/svg.image?=\displaystyle \frac{1}{2}\lim_{ x\to 0}\frac{\sin 6x\cos 2x}{x\cos 10x\cos 2x}$

$https://latex.codecogs.com/svg.image?=\displaystyle \frac{1}{2}\lim_{ x\to 0}\frac{\sin 6x}{x\cos 10x}$

$https://latex.codecogs.com/svg.image?=\displaystyle \frac{1}{2}\lim_{ x\to 0}\frac{\sin 6x}{x}.\displaystyle \lim_{x \to 0}\frac{1}{\cos 10x}$

$https://latex.codecogs.com/svg.image?=\frac{1}{2}.6.1=3$

Kunci jawaban : E

13. Suatu mesin diprogram untuk menggerakkan sebuah alat penggores sedimikan hingga posisi alat tersebut dinyatakan dengan x = 3 cos 4t dan y = 2 cos 3t (posisi dalam satuan cm dan waktu t dalam satuan detik). Kecepatan gerak alat penggores pada saat t dinyatakan dengan $https://latex.codecogs.com/svg.image?v=\sqrt{\left ( \frac{dx}{dt} \right )^{2}+\left ( \frac{dy}{dt} \right )^{2}}$ dalam satuan cm/detik. Besar kecepatan gerak alat tersebut saat $https://latex.codecogs.com/svg.image?t=\frac{\pi }{2}$ detik adalah .....

A. 2 cm/detik

B. $https://latex.codecogs.com/svg.image?\sqrt{13}$ cm/detik

C. 6 cm/detik

D. $https://latex.codecogs.com/svg.image?6\sqrt{5}$ cm/detik

E. 12 cm/detik

Pembahasan

$https://latex.codecogs.com/svg.image?x=3\cos 4t\Rightarrow \frac{dx}{dt}=-12\sin 4t$

$https://latex.codecogs.com/svg.image?y=2\cos 3t\Rightarrow \frac{dy}{dt}=-6\sin 3t$

Substitusikan ke persamaan kecepatan yang diketahui dari soal diatas

$https://latex.codecogs.com/svg.image?v(t)=\sqrt{\left ( \frac{dx}{dt} \right )^{2}+\left ( \frac{dy}{dt} \right )^{2}}$

$https://latex.codecogs.com/svg.image?=\sqrt{\left (-12\sin 4t \right )^{2}+\left (-6\sin 3t\right )^{2}}$

$https://latex.codecogs.com/svg.image?=\sqrt{144\sin^{2}4t+36\sin^{2}3t}$

Kecepatan pada saat $https://latex.codecogs.com/svg.image?t=\frac{\pi }{2}$ detik adalah :

$https://latex.codecogs.com/svg.image?v\left ( \frac{\pi }{2} \right )=\sqrt{144\sin^{2}2\pi +36\sin^{2}\left ( \frac{3}{2}\pi \right )}$

$https://latex.codecogs.com/svg.image?=\sqrt{144(0)^{2}+36(-1)^{2}}$

$https://latex.codecogs.com/svg.image?=\sqrt{36}=6$

Jadi kecepatan penggores saat $https://latex.codecogs.com/svg.image?t=\frac{\pi }{2}$ detik adalah 6 cm/detik.

Kunci jawaban : C

19. Himpunan penyelesaian persamaan $https://latex.codecogs.com/svg.image?\sin \left ( 3x+30^{o} \right )=\frac{1}{2}\sqrt{2}$ pada interval $https://latex.codecogs.com/svg.image?0^{o}\leq x\leq 180^{o}$ adalah ....

A. $https://latex.codecogs.com/svg.image?\left\{5^{o},35^{o} \right\}$

B. $https://latex.codecogs.com/svg.image?\left\{5^{o},125^{o} \right\}$

C. $https://latex.codecogs.com/svg.image?\left\{5^{o},35^{o},65^{o},95^{o} \right\}$

D. $https://latex.codecogs.com/svg.image?\left\{5^{o},35^{o},125^{o},155^{o} \right\}$

E. $https://latex.codecogs.com/svg.image?\left\{5^{o},35^{o},95^{o},155^{o} \right\}$

Pembahasan

Ingat bahwa
$https://latex.codecogs.com/svg.image?\sin x=\sin\alpha \Rightarrow x_{1}=\alpha +k.360^{o}\, \, \mathrm{dan}\, \, x_{2}=(180-\alpha )+k.360^{o}$

Sehingga diperoleh

$https://latex.codecogs.com/svg.image?\sin \left ( 3x+30^{o} \right )=\frac{1}{2}\sqrt{2}$

$https://latex.codecogs.com/svg.image?\sin \left ( 3x+30^{o} \right )=\sin 45^{o}$

maka

* $https://latex.codecogs.com/svg.image?3x+30^{o}=45^{o}+k.360^{o}$

$https://latex.codecogs.com/svg.image?k=0\Rightarrow 3x+30^{o}=45^{o}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 3x=15^{o}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x=5^{o}$

$https://latex.codecogs.com/svg.image?k=1\Rightarrow 3x+30^{0}=45^{o}+360^{o}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 3x+30^{0}=405^{o}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 3x=375^{o}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x=125^{o}$

$https://latex.codecogs.com/svg.image?k=2\Rightarrow 3x+30^{o}=45^{o}+2.360^{o}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 3x+30^{o}=45^{o}+720^{o}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 3x+30^{o}=45^{o}+765^{o}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 3x+30^{o}=765^{o}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 3x=735^{o}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x=245^{o}\, \, (\mathrm{TM})$

** $https://latex.codecogs.com/svg.image?3x+30^{o}=\left ( 180^{o}-45^{o} \right )+k.360^{o}$

$https://latex.codecogs.com/svg.image?3x+30^{o}=135^{o}+k.360^{o}$

$https://latex.codecogs.com/svg.image?k=0\Rightarrow 3x+30^{o}=135^{o}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 3x=105^{o}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x=35^{o}$

$https://latex.codecogs.com/svg.image?k=1\Rightarrow 3x+30^{o}=135^{o}+360^{o}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 3x+30^{o}=495^{o}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 3x=465^{o}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x=155^{o}$

$https://latex.codecogs.com/svg.image?k=2\Rightarrow 3x+30^{o}=135^{o}+2.360^{o}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 3x+30^{o}=135^{o}+720^{o}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 3x+30^{o}=855^{o}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 3x=825^{o}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x=275^{o}\, \, (\mathrm{TM})$

Jadi himpunan penyelesaian dari persamaan trigonometri diatas adalah

$https://latex.codecogs.com/svg.image?HP=\left\{5^{o},35^{o},125^{o},155^{o} \right\}$

Kunci jawaban : D

20 Diketahui segitiga ABC siku-siku di B. Jika $https://latex.codecogs.com/svg.image?\sin A.\sin C=\frac{1}{10}$ dan $https://latex.codecogs.com/svg.image?\sin (A-C)=\frac{2}{5}x$ , nilai x yang memebuhi adalah .....

A. -2

B. $https://latex.codecogs.com/svg.image?-\frac{1}{2}$

C. $https://latex.codecogs.com/svg.image?\frac{1}{4}$

D. $https://latex.codecogs.com/svg.image?\frac{1}{2}$

E. 2

Pembahasan

$https://latex.codecogs.com/svg.image?A+B+C=90^{o}$

Karena $https://latex.codecogs.com/svg.image?B=90^{o}\Rightarrow A+C=90^{o}$

$https://latex.codecogs.com/svg.image?\cos(A+C)=\cos A\cos C-\sin A\sin C$

$https://latex.codecogs.com/svg.image?\cos 90^{o}=\cos A\cos C-\sin A\sin C$

$https://latex.codecogs.com/svg.image?0=\cos A\cos C-\frac{1}{10}$

$https://latex.codecogs.com/svg.image?\cos A\cos C=\frac{1}{10}$

$https://latex.codecogs.com/svg.image?\cos (A-C)=\cos A\cos C+\sin A\sin C$

$https://latex.codecogs.com/svg.image?\cos (A-C)=\frac{1}{10}+\frac{1}{10}$

$https://latex.codecogs.com/svg.image?\cos (A-C)=\frac{2}{10}$

$https://latex.codecogs.com/svg.image?\cos (A-C)=\frac{1}{5}$

Misal $https://latex.codecogs.com/svg.image?A-C=\alpha \Rightarrow \cos \alpha =\frac{1}{5}$

Perhatikan gambar segitiga siku-siku berikut

Dari gambar diperoleh

$https://latex.codecogs.com/svg.image?\sin \alpha =\sin (A-C)=\frac{\sqrt{24}}{5}=\frac{2}{5}\sqrt{6}$

Pada soal diketahui $https://latex.codecogs.com/svg.image?\sin (A-C)=\frac{2}{5}x$ , jadi $https://latex.codecogs.com/svg.image?x=\sqrt{6}$ (untuk A > C) atau $https://latex.codecogs.com/svg.image?x=-\sqrt{6}$ (untuk A < C)

Kunci jawaban : Tidak ada yang benar

23. Diketahui vektor $https://latex.codecogs.com/svg.image?\vec{a}=-2\hat{i}+3\hat{j}+\hat{k}$ dan $https://latex.codecogs.com/svg.image?\vec{b}=4\hat{i}+4\hat{j}+m\hat{k}$ . Jika panjang proyeksi vektor $https://latex.codecogs.com/svg.image?\vec{a}$ pada $https://latex.codecogs.com/svg.image?\vec{b}$ adalah $https://latex.codecogs.com/svg.image?\frac{1}{3}$ , nilai m yang memenuhi adalah ....

A. -7

B. -5

C. 2

D. 5

E. 7

Pembahasan

Diketahui

$https://latex.codecogs.com/svg.image?\vec{a}=\begin{pmatrix}-2 \\ 3\\1\end{pmatrix}$ dan $https://latex.codecogs.com/svg.image?\vec{b}=\begin{pmatrix}4 \\ 4\\m\end{pmatrix}$

Misal $https://latex.codecogs.com/svg.image?\vec{c}$ adalah proyeksi vektor $https://latex.codecogs.com/svg.image?\vec{a}$ pada $https://latex.codecogs.com/svg.image?\vec{b}$ maka $https://latex.codecogs.com/svg.image?\left|\vec{c} \right|=\frac{1}{3}$

Dengan menggunakan rumus panjang proyeksi vektor $https://latex.codecogs.com/svg.image?\vec{a}$ pada $https://latex.codecogs.com/svg.image?\vec{b}$ diperoleh

$https://latex.codecogs.com/svg.image?\left|\vec{c} \right|=\frac{\vec{a}.\vec{b}}{\left|\vec{b} \right|}$

$https://latex.codecogs.com/svg.image?\frac{1}{3}=\frac{(-2)(4)+(3)(4)+(1)(m)}{\sqrt{4^{2}+4^{2}+m^{2}}}$

$https://latex.codecogs.com/svg.image?\frac{1}{3}=\frac{-8+12+m}{\sqrt{16+16+m^{2}}}$

$https://latex.codecogs.com/svg.image?\frac{1}{3}=\frac{4+m}{\sqrt{32+m^{2}}}$ (lakukan perkalian silang)

$https://latex.codecogs.com/svg.image?\sqrt{32+m^{2}}=3(4+m)$

$https://latex.codecogs.com/svg.image?\sqrt{32+m^{2}}=12+3m$ (kedua ruas dikuadratkan)

$https://latex.codecogs.com/svg.image?32+m^{2}=\left ( 12+3m \right )^{2}$

$https://latex.codecogs.com/svg.image?32+m^{2}=144+75m+9m^{2}$

$https://latex.codecogs.com/svg.image?8m^{2}+72m+112=0$ (masing-masing bagi dengan 8)

$https://latex.codecogs.com/svg.image?m^{2}+9m+14=0$

$(m+2)(m+7)=0$

$https://latex.codecogs.com/svg.image?m=-2\, \, \mathrm{atau}\, \, m=-7$

Kunci jawaban : A

Baca Juga :

Pembahasan soal fungsi kuadrat

Pembahasan soal fungsi aljabar, komposisi fungsi dan invers fungsi

Pembahasan soal eksponen dan logaritma

28. Sepasang suami istri merencakan untuk mempunyai 4 orang anak. Jika variabel acak X menyatakan banyak anak perempuan, nilai dari $https://latex.codecogs.com/svg.image?P(x\leq 2)$ adalah ....

A. $https://latex.codecogs.com/svg.image?\frac{4}{16}$

B. $https://latex.codecogs.com/svg.image?\frac{5}{16}$

C. $https://latex.codecogs.com/svg.image?\frac{6}{16}$

D. $https://latex.codecogs.com/svg.image?\frac{10}{16}$

E. $https://latex.codecogs.com/svg.image?\frac{11}{16}$

Pembahasan

Dari empat anak, kemungkinan banyak anak perempuan kurang dari atau sama dengan 2 adalah

0P 4L, 1P 3L, 2P 2L

Dengan menggunakan distribusi binomial diperoleh

$https://latex.codecogs.com/svg.image?0P\, \, 4L\Rightarrow C_{0}^{4}.\left ( \frac{1}{2} \right )^{0}.\left ( \frac{1}{2} \right )^{4}=1.1.\frac{1}{16}=\frac{1}{16}$

$https://latex.codecogs.com/svg.image?1P\, \, 3L\Rightarrow C_{1}^{4}.\left ( \frac{1}{2} \right )^{1}.\left ( \frac{1}{2} \right )^{3}=4.\frac{1}{2}.\frac{1}{8}=\frac{4}{16}$

$https://latex.codecogs.com/svg.image?2P\, \, 2L\Rightarrow C_{2}^{4}.\left ( \frac{1}{2} \right )^{2}.\left ( \frac{1}{2} \right )^{2}=6.\frac{1}{4}.\frac{1}{4}=\frac{6}{16}$

Sehingga $https://latex.codecogs.com/svg.image?P\left ( x\leq 2 \right )=\frac{1}{16}+\frac{4}{16}+\frac{6}{16}=\frac{11}{16}$

Kunci jawaban : E

Soal Uraian

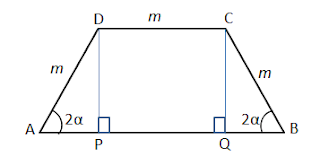
33. Gambar dibawah adalah sebuah trapesium ABCD dengan AD = CD = BC = m cm, dan $https://latex.codecogs.com/svg.image?\angle DAB= \angle CBA=2\alpha$ ( $https://latex.codecogs.com/svg.image?\alpha$ adalah sudut lancip).

Berapakah luas maksimum trapesium tersebut (dalam m $https://latex.codecogs.com/svg.image?\mathrm{cm}^{2}$ ). Tuliskan langkah penyelesaiannya !

Pembahasan

Gambar diatas kita tambah beberapa garis bantu, seperti pada gambar berikut !

Perhatikan segitiga APD dan segitiga QBC, dari segitiga tersebut diperoleh

AP = QB = m cos 2 $https://latex.codecogs.com/svg.image?\alpha$

PD = QC = m sin 2 $https://latex.codecogs.com/svg.image?\alpha$

AP = AP + PQ + QB = m + 2m cos 2 $https://latex.codecogs.com/svg.image?\alpha$

Luas trapesium adalah

$https://latex.codecogs.com/svg.image?L=\frac{1}{2}(AB+CD).PD$

$https://latex.codecogs.com/svg.image?=\frac{1}{2}(m+2m\cos 2\alpha +m).m\sin 2\alpha$

$https://latex.codecogs.com/svg.image?=\frac{1}{2}(2m+2m\cos 2\alpha).m\sin 2\alpha$

$https://latex.codecogs.com/svg.image?=\frac{1}{2}2(m+m\cos 2\alpha).m\sin 2\alpha$

$https://latex.codecogs.com/svg.image?=(m+m\cos 2\alpha).m\sin 2\alpha$

$https://latex.codecogs.com/svg.image?=m^{2}\sin 2\alpha +m^{2}\sin 2\alpha \cos 2\alpha$

$https://latex.codecogs.com/svg.image?=m^{2}\sin 2\alpha +\frac{1}{2}m^{2}(2\sin 2\alpha \cos 2\alpha)$

$https://latex.codecogs.com/svg.image?=m^{2}\sin 2\alpha +\frac{1}{2}m^{2}\sin 4\alpha$

Luas maksimum akan dipeeroleh jika

$https://latex.codecogs.com/svg.image?L'=\frac{dL}{d\alpha }=0$

$https://latex.codecogs.com/svg.image?2m^{2}\cos 2\alpha +2m^{2}\cos 4a=0$

$https://latex.codecogs.com/svg.image?2m^{2}(\cos 2\alpha +\cos 4a)=0$

$https://latex.codecogs.com/svg.image?\cos 2\alpha +\cos 4a=0$

$https://latex.codecogs.com/svg.image?\cos 2\alpha +2\cos^{2}2\alpha -1=0$

$https://latex.codecogs.com/svg.image?2\cos^{2}2\alpha +\cos 2\alpha-1=0$

$https://latex.codecogs.com/svg.image?(2\cos 2\alpha -1)(\cos 2\alpha +1)=0$

$https://latex.codecogs.com/svg.image?\cos 2\alpha=\cos 60^{o}$ $https://latex.codecogs.com/svg.image?\cos 2\alpha=\frac{1}{2}\, \, \mathrm{atau}\, \, \cos 2\alpha=-1$

Ingat kembali bahwa
$https://latex.codecogs.com/svg.image?\cos x=\cos \alpha \Leftrightarrow x=\pm \alpha +k.360^{o}$

Untuk $https://latex.codecogs.com/svg.image?\cos 2\alpha=\frac{1}{2}$

$https://latex.codecogs.com/svg.image?\cos 2\alpha=\cos 60^{o}$

$https://latex.codecogs.com/svg.image?2\alpha =\pm 60^{o}+k.360^{o}$

* $https://latex.codecogs.com/svg.image?2\alpha =60^{o}+k.360^{o}$

$https://latex.codecogs.com/svg.image?k=0\Rightarrow 2\alpha =60^{o}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \alpha =30^{o}$

$https://latex.codecogs.com/svg.image?k=1\Rightarrow 2\alpha =60^{o}+360^{o}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 2\alpha =420^{o}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \alpha =210^{o}\left ( \mathrm{TM} \right )$

* $https://latex.codecogs.com/svg.image?2\alpha =-60^{o}+k.360^{o}$

$https://latex.codecogs.com/svg.image?k=0\Rightarrow \alpha =-30^{o}(\mathrm{TM})$

Untuk $https://latex.codecogs.com/svg.image?\cos 2\alpha =-1$

$https://latex.codecogs.com/svg.image?\cos 2\alpha =\cos 180^{o}$

$https://latex.codecogs.com/svg.image?2\alpha =\pm 180^{o}+k.360^{o}$

* $https://latex.codecogs.com/svg.image?2\alpha =180^{o}+k.360^{o}$

$https://latex.codecogs.com/svg.image?k=0\Rightarrow 2\alpha =180^{o}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \alpha =90^{o}(\mathrm{TM})$

untuk yang lain tidak dicek karena tidak memenuhi (silahkan bisa cek sendiri)

Karena syarat $https://latex.codecogs.com/svg.image?\alpha$ adalah sudut lancip maka yang memenuhi adalah $https://latex.codecogs.com/svg.image?\alpha =30^{o}$

Sehingga luas maksimum trapesium adalah

$https://latex.codecogs.com/svg.image?L=m^{2}\sin 2\alpha +\frac{1}{2}m^{2}\sin 4\alpha$

$https://latex.codecogs.com/svg.image?\alpha =30^{o}\Rightarrow L_{maks}=m^{2}\sin 60^{o}+\frac{1}{2}m^{2}\sin 120^{o}$

$https://latex.codecogs.com/svg.image?=m^{2}\left ( \frac{1}{2}\sqrt{3} \right )+\frac{1}{2}m^{2}\left ( \frac{1}{2}\sqrt{3}\right )$

$https://latex.codecogs.com/svg.image?=\frac{1}{2}\sqrt{3}m^{2}+\frac{1}{4}\sqrt{3}m^{2}$

$https://latex.codecogs.com/svg.image?=\frac{3}{4}\sqrt{3}m^{2}$

Jadi luas maksimum trapesium tersebut adalah $https://latex.codecogs.com/svg.image?\frac{3}{4}\sqrt{3}m^{2}$ $https://latex.codecogs.com/svg.image?\mathrm{cm}^{2}$ .

Soal Anchor USBN Matematika Minat 2019 dan Pembahasannya

Apa itu soal anchor USBN ?

Soal Pilihan Ganda

Soal Uraian

Post a Comment

Post a Comment

Contact Form

Soal Anchor USBN Matematika Minat 2019 dan Pembahasannya

Apa itu soal anchor USBN ?

Soal Pilihan Ganda

Soal Uraian

You might like

Post a Comment

Post a Comment

Contact Form