Memahami Limit Fungsi secara Intuitif

Definisi (Pengertian limit secara intuitif)

Misalkan f sebuah fungsi  dan misalkan L dan c anggota himpunan bilangan real.  jika dan hanya jika f(x) mendekati L untuk x mendekati c

Catatan :

1.  dibaca limit fungsi f(x) sama dengan L untuk x mendekati c
2. Kita menyatakan bahwa f(x) mendekati L ketika x mendekati c yang terdefinisi pada selang/interval yang memuat c kecuali mungkin di c sendiri.
3. Limit fungsi mempunyai sifat :  jika dan hanya jika 

Soal dan Pembahasan

Perhatikan beberapa soal berikut

1. Jika diketahui  , tentukan nilai f(x) pada saat x mendekati 2

 Perhatikan tabel berikut

x	1	1,5	1,7	1,9	1,99	1,999	…	2	…	2,001	2,01	2,1	2,5	2,7	3
y	0	0,5	0,7	0,9	0,99	0,999	…	1	…	1,001	1,01	1,1	1,5	1,7	2

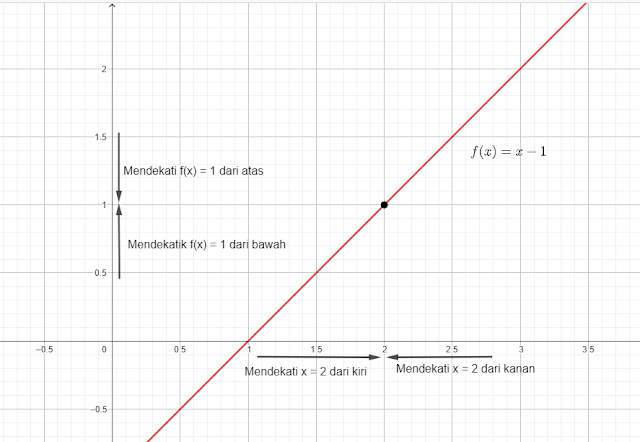
Gambar grafik fungsi tersebut adalah

Jika diamati tabel dan grafik diatas, maka ada beberapa hasil pengamatan sebagai berikut.

1. Terdapat tak hingga bilangan ril yang mendekati x = 2
2. Setiap titik di sumbu x (daerah asal) mumpunyai pasangan di sumbu y (daerah hasil).
3. Setiap nilai pada fungsi mendekati 1 pada saat x mendekati 2 baik dari kiri maupun dari kanan

Dari hal-hal diatas dinyatakan bahwa 

2. Jika diketahui , tentukan nilai f(x) pada saat x mendekati 1.

Perhatikan bahwa fungsi f(x) tidak terdefinisi pada x = 1, tetapi yang akan diperhatikan bukan pada x =1 melainkan nilai x yang mendekati x =1 baik dari kiri maupun kanan. Sehingga bentuk  bisa disederhanakan dengan cara memfaktorkan menjadi 

Perhatikan tabel berikut

x	0	0,5	0,7	0,9	0,99	0,999	…	1	…	1,001	1,01	1,1	1,5	1,7	2
y	1	1,5	1,7	1,9	1,99	1,999	…	?	…	2,001	2,01	2,1	2,5	2,7	3

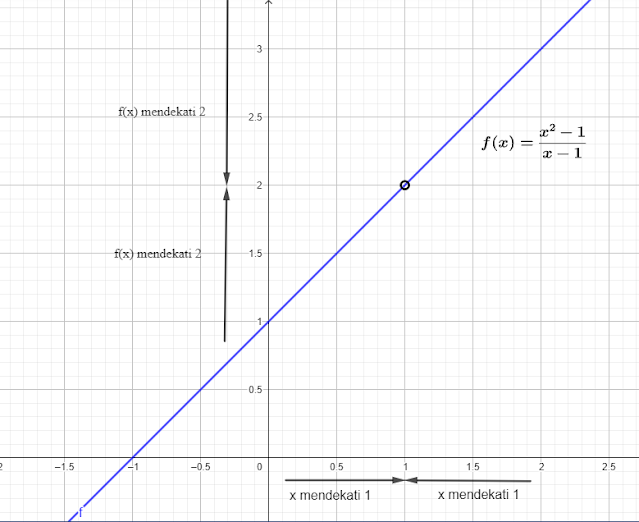
Perhatikan perhatikan pola nilai y dari kiri mendekati sebuah nilai secara terus menerus yaitu y = 2, begitu juga nilai y dari kanan mendekati sebuah nilai secara terus menerus yaitu y = 2

Perhatikan juga grafik dari fungsi diatas

Dari tabel dan grafik diatas kita katakan bahwa 

3. Jika , tentukan nilai f(x) pada saat x mendekati 1

Perhatikan tabel berikut

x	0	0,5	0,7	0,9	0,99	0,999	…	1	…	1,001	1,01	1,1	1,5	1,7	2
y	0	0,25	0,49	0,81	0,98	0,998	…	?	…	2,001	2,01	2,1	2,5	2,7	3

Berdasarkan tabel diatas, nilai f(x) akan mendekati 1 pada saat x mendekati 1 dari kiri, sementara nilai f(x) endekati 2 pada saat x mendekati 1 dari kanan.

Perhatikan juga grafik fungsi berikut

Kita bisa menuliskan bahwa 

 dan  , sehinga limit kiri tidak sama dengan limit kanan, maka 

Perhatikan bahwa tanda bundaran penuh menunjukkan f(x) memiliki nilai di titik itu dan tanda bundaran kosong menunjukkan f(x) tidak memiliki nilai di titik itu

4. Perhatikan gambar berikut

Dari gambar diatas tentukan :

1. Nilai , , , , , dan 

2. Nilai f(-3), f(1) dan f(4)

Pembahasan

1. , , ,  dan 

2. f(-3) = 5, f(1) = 3 dan f(4) = tidak ada

5. Perhatikan gambar berikut

Dari gambar diatas manakan yang memiliki limir pada saat x mendekati c

Pembahasan

Gambar A

, sehingga 

Gambar B

 , sehingga 

Gambar C

, sehingga  walaupun f(c) tidak ada

Gambar D

 , sehingga  walaupun f(c) ada

6. (Soal pada kalkulus 1 halaman 114 nomor 27) Perhatikan gambar berikut

Untuk fungsi f yang digambarkan grafik diatas, cari limit yang ditunjukkan atau nilai fungsi, atau nyatakan bahwa limit tersebut tidak ada.

a. 

b. f(-3)

c. f(-1)

d. 

e. f(1)

f. 

g. 

h. 

Pembahasan

a.  karena 

b. Perhatikan tanda bundaran kosong pada garis menunjukkan bahwa f(-3) pada titik itu tidak memiliki nilai tetapi dibawahnya ada bundaran penuh yang menunjukkan bahwa f(-3) memiliki nilai pada titik itu yaitu f(-3) = 1

c. f(-1) = tidak ada

d.  = ada (Nilai sebenarnya silahkan diperkirakan karena pada grafik tidak ditunjukkan dengan jelas nilainya)

e. f(1) = 2

f.  = tidak ada

g.  = 2

h.  = 1

Demikian pembahasan singkat tentang bagaimana cara memahami limit fungsi secara intuitif. Semoga bermanfaat. Komentar dan saran sangat diharapkan untuk pengembangan website ini. Terimakasih