Komposisi Transformasi Dengan Matriks - merupakan materi matematika wajib kelas XI semua jurusan yang merupakan kelanjutan dari materi komposisi transformasi geometri yang sudah diajarkan di SMP/MTs. Berikut penjelasan Komposisi Transformasi dengan Matriks.
.png) |
| sumber : www.google.com dan diseain menggunakan canva for education |
PENGERTIAN
Misalkan suatu benda atau bangun dilakukan komposisi transformasi. Pertama ditansformasi yang bersesuaian dengan matriks
, dilanjutkan dengan transformasi
yang bersesuaian dengan matriks
, dan dilanjutkan lagi dengan transformasi
yang bersesuaian dengan matriks
. Penulisan komposisinya yaitu
Perlu diperhatikan bahwa penulisannya dibalik sesuai dengan urutan pengerjaannya.
MENENTUKAN BAYANGAN
Bentuk umum bayangan dari komposisi transformasi dengan matriks adalah
1. Bayangan dengan titik pusat O(0,0)
2. Bayangan dengan titik pusat P(a,b)
MATRIKS TRANSFORMASI (M)
Untuk memudahkan dalam pengerjaan masalah transformasi berikut diberikan matriks transformasi (M)
Refleksi atau Pencerminan
1. Matriks transformasi refleksi atau pencerminan terhadap pusat koordinat O(0,0)
2. Matriks tranformasi refleksi atau pencerminan terhadap sumbu x
3. Matriks tranformasi refleksi atau pencerminan terhadap sumbu y
4. Matriks tranformasi refleksi atau pencerminan terhadap garis y = x
5. Matriks tranformasi refleksi atau pencerminan terhadap garis y = -x
6. Matriks tranformasi refleksi atau pencerminan terhadap garis y = mx + c
Translasi
Matriks transformasi dari translasi adalah :
Rotasi
Matriks transformasi dari rotasi dengan besar sudut adalah :
Dilatasi
Matriks transformasi dari dilatasi dengan faktor skala k adalah :
SYARAT MATRIKS TRANSFORMASI BISA LANGSUNG DIKALIKAN
Syarat supaya dua atau lebih matriks transformasi bisa dikalikan dan tidak mengerjakannya satu persatu adalah sebagai berikut.
1. Matriks transformasinya harus berordo 2 x 2.
2. Jika memiliki pusat (titik acuan seperti rotasi dan dilatasi), maka titik pusatnya harus sama.
3. Jika pada transformasi tidak disebutkan titik pustnya seperti refleksi, maka titik pusatnya dianggap O(0,0) dan matriks transformasinya langsung dapat dikalikan dengan matriks transformasi yang titik pusatnya O(0,0) juga atau yang tidak disebutkan titik pusatnya.
Catatan
Ketiga syarat diatas harus terpenuhi untuk bisa langsung mengalikan dua jenis matriks transformasi atau lebih.
Contoh Soal dan Pembahasan
1. Persamaan garis 3x – 2y dicerminkan terhadap sumbu x, kemudian dilanjutkan dengan rotasi sejauh searah jarum jam, dan dilanjutkan lagi dengan dilatasi dengan faktor skala -3. Tentukan bayangan dari persamaan garis tersebut.
Pembahasan
Matriks dicerminkan terhadap sumbu x, rotasi dan dilatasi pasti berordo 2 x 2. Pada soal juga tidak disebutkaan titik pusat transformasinya, sehingga titik pusatnya dianggap sama yaitu O(0,0). Ini artinya ketiga matriks transformasi dapat dikalikan langsung tanpa harus mengerjakan satu persatu.
a. Menentukan matriks transformasi masing-masing
: percerminan terhadap sumbu x, maka
: Rotasi sejauh
terhadap sumbu x, maka
: dilatasi dengan faktor skala -3, maka
b. Menentukan bayangan
Sehingga diperoleh :
Substitusikan nilai x dan y ke persamaan garis yang akan dicari bayangannya
Jadi persamaan bayangan garis yang ditanyakan adalah
2. Tentukan persamaan bayangan jika ditranslasi sejauh
dan dilanjutkan dengan pencerminan terhadap garis y = - x
Pembahasan
Matriks translasi tidak berordo 2 x 2, sehingga tidak memenuhi syarat untuk melakukan perkalian langsung kedua matriks transformasinya. Ini artinya kita akan mengerjakan satu persatu.
a. Pertama di ditranslasi
b. Kedua dicerminkan terhadap garis y = - x
Matriks transformasinya adalah sehingga diperoleh :
sehingga diperoleh
Substitusikan nilai x dan y ke persamaan garis yang akan dicari bayangannya
Jadi persamaan bayangan garis tersebut adalah
Demikian pembahasan tentang komposisi transformasi dengan matriks dan pembahasan soal, semoga bermanfaat.



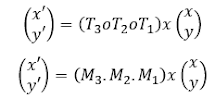



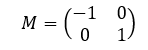
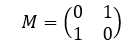

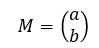

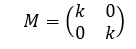
إرسال تعليق
Terimakasih untuk anda telah berkomentar di postingan ini