Pertidaksamaan Logaritma dan Pembahasan Soal

Pada pembahasan sebelumnya kita sudah membahas persamaan logaritma dan fungsi logaritma, pada bahasan ini kita akan membahas pertidaksamaan logaritma dan pembahasan soal. Yang perlu dipahami dalam pertidaksamaan logaritma adalah sifat-sifat pertidaksamaan logaritma dan sifat-sifat yang berlaku pada logaritma. Untuk lebih jelasnya simaklah pembahasan pertidaksamaan logaritma dan pembahasan soal berikut.

Sifat-sifat yang berlaku pada pertidaksamaan logaritma adalah sebagai berikut

Jika a > 0 dan $https://latex.codecogs.com/svg.image?^{a}\log f(x)\geq \, ^{a}\log g(x)$ maka $https://latex.codecogs.com/svg.image?f(x)\geq g(x)$
Jika a > 0 dan $https://latex.codecogs.com/svg.image?^{a}\log f(x)\leq \, ^{a}\log g(x)$ maka $https://latex.codecogs.com/svg.image?f(x)\leq g(x)$
Jika 0 < a < 1 dan $https://latex.codecogs.com/svg.image?^{a}\log f(x)\geq \, ^{a}\log g(x)$ maka $https://latex.codecogs.com/svg.image?f(x)\leq g(x)$
Jika 0 < a < 1 dan $https://latex.codecogs.com/svg.image?^{a}\log f(x)\leq \, ^{a}\log g(x)$ maka $https://latex.codecogs.com/svg.image?f(x)\geq g(x)$

Dari sifat-sifat diatas berlaku juga untuk tanda ketidaksamaan > dan <.

Contoh Soal dan Pembahasan

1. Tentukan himpunan penyelesaian dari $https://latex.codecogs.com/svg.image?-4<\, \, \, ^{2}\log \left ( 4x-1 \right )<4$

Pembahasan

$https://latex.codecogs.com/svg.image?-4<\, \, \, ^{2}\log \left ( 4x-1 \right )<4$

$https://latex.codecogs.com/svg.image?\Leftrightarrow -4\, ^{2}\log 2<\, \, \, ^{2}\log \left ( 4x-1 \right )<4\, \, ^{2}\log 2$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, ^{2}\log 2^{-4}<\, \, \, ^{2}\log \left ( 4x-1 \right )<\, \, ^{2}\log 2^{4}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, 2^{-4}<4x-1<2^{4}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, \frac{1}{16}<4x-1<16$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, \frac{1}{16}+1<4x-1+1<16+1$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, \frac{17}{16}<4x<17$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, \frac{17}{16}.\frac{1}{4}<\frac{1}{4}.4x<17.\frac{1}{4}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, \frac{17}{64}<x<\frac{17}{4}$

Jadi himpunan penyelesaian dari pertidaksamaan logaritma diatas adalah $https://latex.codecogs.com/svg.image?\left\{x\, |\, \frac{17}{64}<\, x\, <\frac{17}{4} \right\}$

2. Tentukan penyelesaian dari pertidaksamaan logaritma $https://latex.codecogs.com/svg.image?^{2}\log \left ( x^{2}+5x+6 \right )<1$

Pembahasan

$https://latex.codecogs.com/svg.image?^{2}\log \left ( x^{2}+5x+6 \right )<1$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, ^{2}\log \left ( x^{2}+5x+6 \right )<\, \, ^{2}\log 2$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, x^{2}+5x+6<2$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, x^{2}+5x+4<0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, \left ( x+1 \right )\left ( x+4 \right )<0$

Pembuat nol fungsi

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, \left ( x+1 \right )\left ( x+4 \right )=0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, x=-1\, \, atau\, \, x=-4$

Masukkan nilai x diatas ke garis bilangan

Pertidaksamaan Logaritma dan Pembahasan Soal

Nilai x yang memenuhi adalah -4 < x < -1

Syarat $https://latex.codecogs.com/svg.image?^{2}\log \left ( x^{2}+5x+6 \right )$ terdefinisi adalah

$https://latex.codecogs.com/svg.image?x^{2}+5x+6>0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, \left ( x+2 \right )\left ( x+3 \right )>0$

Pembuat nol fungsi

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, \left ( x+2 \right )\left ( x+3 \right )=0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, x=-2\, \, atau\, \, x=-3$

Masukkan nilai x yang diperoleh dari langkah diatas ke garis bilangan

Diperoleh nilai x yang memenuhi adalah x < -3 atau x > -2

Untuk menentukan daerah hasil iriskan kedua garis bilangan diatas dan daerah yang beririsan merupakan daerah penyelesaian dari pertidaksamaan logaritma diatas.

Dari garis bilangan diatas diperoleh nilai x yang memenuhi adalah $https://latex.codecogs.com/svg.image?-4<x<-3\, \, \mathrm{atau}\, \, -2<x<-1$

Jadi himpunan penyelesaian dari pertidaksamaan logaritma diatas adalah $https://latex.codecogs.com/svg.image?\left\{x\, |-4<x<-3\, \, \mathrm{atau}\, \, -2<x<-1 \right\}$

3. Tentukan himpunan penyelesaian dari $https://latex.codecogs.com/svg.image?^{\frac{1}{2}}\log \left ( x^{2}-5x+4 \right )>-2$

Pembahasan

$https://latex.codecogs.com/svg.image?^{\frac{1}{2}}\log \left ( x^{2}-5x+4 \right )>-2$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, ^{\frac{1}{2}}\log \left ( x^{2}-5x+4 \right )>-2\, \, ^{\frac{1}{2}}\log \frac{1}{2}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, ^{\frac{1}{2}}\log \left ( x^{2}-5x+4 \right )>\, \, ^{\frac{1}{2}}\log \left ( \frac{1}{2} \right )^{-2}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, ^{\frac{1}{2}}\log \left ( x^{2}-5x+4 \right )>\, \, ^{\frac{1}{2}}\log (2)^{2}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, ^{\frac{1}{2}}\log \left ( x^{2}-5x+4 \right )>\, \, ^{\frac{1}{2}}\log 4$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, x^{2}-5x+4>\, \,4$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, x^{2}-5x>0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, x\left (x-5 \right )>0$

Pembuat nol fungsi

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, x\left (x-5 \right )=0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, x=0\, \, \mathrm{atau}\, \, x=5$

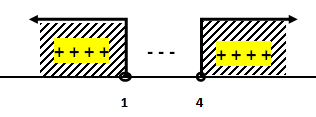
Masukkan nilai x ke garis bilangan

dari garis bilangan diperoleh nilai x yang memenuhi adalah x < 0 atau x > 5

Syarat $https://latex.codecogs.com/svg.image?^{\frac{1}{2}}\log \left ( x^{2}-5x+4 \right )$ terdefinisi adalah

$https://latex.codecogs.com/svg.image?x^{2}-5x+4>0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, \left ( x-1 \right )\left ( x-4 \right )>0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, \left ( x-1 \right )\left ( x-4 \right )=0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, x=1\, \, \mathrm{atau}\, \, x=4$

Masukkan nilai x ke garis bilangan

Untuk menentukan daerah hasil iriskan kedua garis bilangan diatas dan daerah yang beririsan merupakan daerah penyelesaian dari pertidaksamaan logaritma diatas.

Dari garis bilangan diatas terlihat bahwa nilai x yang memenuhi pertidaksamaan logaritma diatas adalah x < 0 atau x > 5

Jadi himpunan penyelesaian dari pertidaksamaan logaritma diatas adalah {x | x < 0 atau x > 5}.

4. Tentukan himpunan penyelesaian dari pertidaksamaan logaritma $https://latex.codecogs.com/svg.image?x^{2\log x}-11x^{\log x}+10<0$

Pembahasan

$https://latex.codecogs.com/svg.image?x^{2\log x}-11x^{\log x}+10<0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, \left ( x^{\log x} \right )^{2}-11x^{\log x}+10<0$

Misal $https://latex.codecogs.com/svg.image?x^{\log x}=y$ , diperoleh pertidaksamaan kuadrat berikut

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, y^{2}-11y+10<0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, \left ( y-1 \right )\left ( y-10 \right )<0$

Pembuat nol fungsi

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, \left ( y-1 \right )\left ( y-10 \right )=0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, y=1\, \, \mathrm{atau}\, \, y=10$

Masukkan nilai y ke garis bilangan

Dari garis bilangan diperoleh nilai y yang memenuhi pertidaksamaan adalah 1 < y < 10

Substitusi nilai y ke permisalan

$https://latex.codecogs.com/svg.image?y=1\Rightarrow x^{\log x}=1$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, x^{\log x}=x^{0}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, \log x=0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, x=1$

$https://latex.codecogs.com/svg.image?y=10\Rightarrow x^{\log x}=10$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, ^{x}\log 10=\log x$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \,\frac{\log 10}{\log x}=\log x$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \,\frac{1}{\log x}=\log x$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 1=\log x\log x$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 1=\left ( \log x \right )^{2}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow 1^{2}=\left ( \log x \right )^{2}$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \log x = 1$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \log x = \log 10$

$https://latex.codecogs.com/svg.image?\Leftrightarrow x =10$

Dengan memperhatikan bentuk interval nilai y yaitu 1 < y < 10, maka interval nilai x adalah 1 < x < 10

Syarat log x terdefinisi adalah x > 0

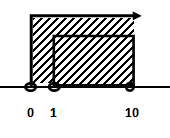
Iriskan semua interval x di garis bilangan

Dari garis bilangan terlihat bahwa nilai x yang memenuhi pertidaksamaan logaritma diatas adalah 1 < x < 10

Jadi himpunan penyelesaian pertidaksamaan logaritma diatas adalah {x | 1 < x < 10}.

Baca Juga :

Persamaan logaritma

Fungsi logaritma

Persamaan eksponen dan pembahasan soal

Fungsi eksponen

Pertidaksamaan eksponen dan pembahasan soal

5. Tentukan nilai x yang memenuhi pertidaksamaan logaritma $https://latex.codecogs.com/svg.image?^{\frac{1}{2}}\log \left ( x^{2}-3 \right )<0$

Pembahasan

$https://latex.codecogs.com/svg.image?^{\frac{1}{2}}\log \left ( x^{2}-3 \right )<0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, ^{\frac{1}{2}}\log \left ( x^{2}-3 \right )<\, ^{\frac{1}{2}}\log 1$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, x^{2}-3<1$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, x^{2}-4<0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, \left ( x-2 \right )\left ( x+2 \right) <0$

Pembuat nol fungsi

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, \left ( x-2 \right )\left ( x+2 \right) =0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, x=2\, \, \mathrm{atau}\, \, x=-2$

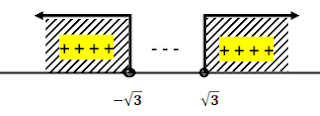
Masukkan nilai x ke garis bilangan

Dari garis bilangan diatas diperoleh nilai x adalah -2 < x < 2

Syarat $https://latex.codecogs.com/svg.image?^{\frac{1}{2}}\log \left ( x^{2}-3 \right )$ terdefinisi adalah

$https://latex.codecogs.com/svg.image?x^{2}-3>0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, \left ( x+\sqrt{3} \right )\left ( x-\sqrt{3} \right )>0$

pembuat nol fungsi

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, \left ( x+\sqrt{3} \right )\left ( x-\sqrt{3} \right )=0$

$https://latex.codecogs.com/svg.image?\Leftrightarrow \, x=-\sqrt{3}\, \, \mathrm{atau}\, \, x=\sqrt{3}$

Masukkan nilai x ke garis bilangan

Dari garis bilangan diperoleh nilai x adalah $https://latex.codecogs.com/svg.image?x=-\sqrt{3}\, \, \mathrm{atau}\, \, x=\sqrt{3}$

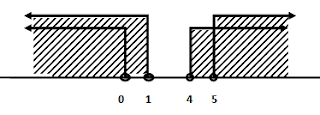
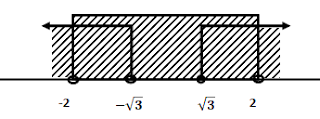
Iriskan nilai x dari kedua garis bilangan diatas

Dari garis bilangan diatas terlihat bahwa nilai x yang memenuhi adalah $https://latex.codecogs.com/svg.image?-2<x<-\sqrt{3}$ atau $https://latex.codecogs.com/svg.image?\sqrt{3}<x<2$

Pertidaksamaan Logaritma dan Pembahasan Soal

Contoh Soal dan Pembahasan

Post a Comment

إرسال تعليق

نموذج الاتصال

Pertidaksamaan Logaritma dan Pembahasan Soal

Contoh Soal dan Pembahasan

You might like

Post a Comment

إرسال تعليق

نموذج الاتصال