Limit Tak Hingga dan Limit di Tak Hingga dan Pembahasan Soal

A. Limit Tak Hingga **(infinity limits)**

Untuk membahas apa itu limit tak hingga perhatikan grafik fungsi berikut

Dari grafik fungsi $f(x)=\frac{1}{x}$ terlihat bahwa nilai f(x) akan menuju positif tak hingga saat x menuju 2 dari arah kanan sementara nilai f(x) akan menuju negatif tak hingga saat x menuju 2 dari arah kiri. Kondisi ini menandakan bahwa f(x) tidak menuju nilai tertentu jika x menuju 2, sehingga dikatakatan $\displaystyle \lim_{x \to 0}\frac{1}{x}$ tidak ada.

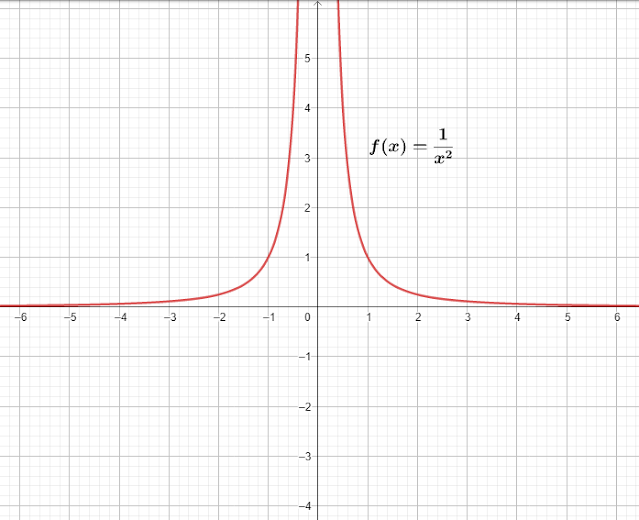
Perhatikan pula grafik fungsi $f(x)=\frac{1}{x^{2}}$ berikut

Dengan melihat grafik jelas bahwa nilai f(x) akan menuju positif tak hingga baik x menuju 2 dari arah kanan maupun dari arah kiri. Ini berarti $\frac{1}{x^{2}}\to \infty$ jika x → 2. Walaupun dalam hal ini f(x) tidak menuju pada nilai atau bilangan tertentu ketika x menuju 2, namun dalam kasus ini f(x) mempunyai limit di tak hingga. Inilah sebenarnya pengertian limit tak hingga. Apabila dituliskan maka penyajiannya menjadi $\displaystyle \lim_{x \to 0}\frac{1}{x^{2}}=\infty$ .

Kesimpulan

Bentuk dari limit tak hingga adalah $\displaystyle \lim_{x \to c}f(x)=\infty$

**B. Limit di Tak Hingga (limits at infinity)**

Perhatikan grafik fungsi berikut

Dengan mencermati grafik tersebut orang akan menyimpulkan bahwa f(x) → 1 apabila x → ∞. Dalam hal ini ditulis dengan $\displaystyle \lim_{x \to \infty }\frac{x}{x+1}=1$

Dari penjelasan diatas diperoleh bahwa limit di tak hingga sangat berbeda dengan limit tak hingga. Perbedaan utamanya terletak pada bilangan yang didekati dan hasil limitnya. Untuk limit tak hingga berkaitan dengan hasil limitnya ∞, sementara untuk limit di tak hingga variabel independennya yang mendekati tak hingga. Coba bandingkan.

$\displaystyle \lim_{x \to c }f(x)=\infty$ (disebut limit tak hingga)

$\displaystyle \lim_{x \to \infty }f(x)=L$ (disebut limit di tak hingga)

C. Menenetukan nilai limit di tak hingga pada fungsi aljabar

1. Menyelesaikan Bentuk $\frac{f(x)}{g(x)}$

Jika diketahui

$f(x)=ax^{m}+a_{1}x^{m-1}+a_{2}x^{m-2}+...$ dan

$g(x)=bx^{n}+b_{1}x^{n-1}+b_{2}x^{n-2}+...$ , maka

$\displaystyle \lim_{x \to \infty }\frac{f(x)}{g(x)}$ dapat diselesaikan dengan dua cara yaitu

1. Membagi semua suku dengan variabel pangkat tertinggi dan lakukan operasi aljabar lainnya dengan berpedoman pada $\displaystyle \lim_{x \to \infty }\frac{1}{x^{n}}=0$

2. Menggunakan rumus yaitu

$\displaystyle \lim_{x \to \infty }\frac{ax^{m}+a_{1}x^{m-1}+a_{2}x^{m-2}+...}{bx^{n}+b_{1}x^{n-1}+b_{2}x^{n-2}+...}=\left\{\begin{matrix}0,\, jika\, m<n \\ \frac{a}{b},\, jika\, m=n\\\infty ,\, jika\, m>n\end{matrix}\right.$

Contoh Soal dan Pembahasan

Tentukan nilai limit berikut

1. $\displaystyle \lim_{x \to \infty }\frac{3x^{2}-4x+6}{2x^{2}+x-5}$

2. $\displaystyle \lim_{x \to \infty }\frac{2x^{2}+x}{4x^{3}+1}$

3. $\displaystyle \lim_{x \to \infty }\frac{x^{3}+4x^{2}+6}{3x^{2}+2x-1}$

4. $\displaystyle \lim_{x \to \infty }\frac{3x^{3}-2x^{2}}{2x^{3}+x}$

5. $\displaystyle \lim_{x \to \infty }\frac{x^{3}-x}{2x^{4}+1}$

6. $\displaystyle \lim_{x \to \infty }\frac{2x^{5}+x^{3}}{x^{3}-x^{2}+1}$

Pembahasan

1. $\displaystyle \lim_{x \to \infty }\frac{3x^{2}-4x+6}{2x^{2}+x-5}$

Cara 1 : Membagi suku-suku dengan variabel pangkat tertinggi

Variabel pangkat tertinggi adalah $x^{2}$ , sehingga diperoleh

$\displaystyle \lim_{x \to \infty }\frac{3x^{2}-4x+6}{2x^{2}+x-5}=\displaystyle \lim_{x \to \infty }\frac{\frac{3x^{2}}{x^{2}}-\frac{4x}{x^{2}}+\frac{6}{x^{2}}}{\frac{2x^{2}}{x^{2}}+\frac{x}{x^{2}}-\frac{5}{x^{2}}}$

$=\displaystyle \lim_{x \to \infty }\frac{3-\frac{4}{x}+\frac{6}{x^{2}}}{2+\frac{1}{x}-\frac{5}{x^{2}}}$

Dengan berpedoman pada $\displaystyle \lim_{x \to \infty }\frac{1}{x^{n}}=0$ , maka

$=\frac{3-0+0}{2+0-0}=\frac{2}{3}$

Cara 2 : Menggunakan rumus

Bentuk $\displaystyle \lim_{x \to \infty }\frac{3x^{2}-4x+6}{2x^{2}+x-5}$ memiliki pangkat variabel tertinggi pembilang sama dengan pangkat variabel tertinggi penyebut, maka berdasarkan rumus diatas diperoleh hasil limit tak hingganya adalah Koefesien variabel pangkat tertinggi pembilang dibagi koefesien variabel pangkat tertinggi penyebut, yaitu :

$\displaystyle \lim_{x \to \infty }\frac{3x^{2}-4x+6}{2x^{2}+x-5}=\frac{3}{2}$

2. $\displaystyle \lim_{x \to \infty }\frac{2x^{2}+x}{4x^{3}+1}$

Cara 1 : Membagi suku-suku dengan variabel pangkat tertinggi

Variabel pangkat tertinggi adalah $x^{3}$ sehingga diperoleh

$\displaystyle \lim_{x \to \infty }\frac{2x^{2}+x}{4x^{3}+1}=\displaystyle \lim_{x \to \infty }\frac{\frac{2x^{2}}{x^{3}}+\frac{x}{x^{3}}}{\frac{4x^{3}}{x^{3}}+\frac{1}{x^{3}}}$

$=\displaystyle \lim_{x \to \infty }\frac{\frac{2}{x}+\frac{2}{x^{2}}}{4+\frac{1}{x^{3}}}$

$=\frac{0+0}{4+0}=\frac{0}{4}=0$

Cara 2 : Menggunakan rumus

Bentuk $\displaystyle \lim_{x \to \infty }\frac{2x^{2}+x}{4x^{3}+1}$ memiliki pangkat variabel tertinggi pembilang lebih kecil dari pangkat variabel tertinggi penyebut, sehingga berdasarkan rumus diatas diperoleh

$\displaystyle \lim_{x \to \infty }\frac{2x^{2}+x}{4x^{3}+1}=0$

3. $\displaystyle \lim_{x \to \infty }\frac{x^{3}+4x^{2}+6}{3x^{2}+2x-1}$

Cara 1 : Membagi suku-suku dengan variabel pangkat tertinggi

Variabel pangkat tertinggi adalah $x^{3}$ sehingga diperoleh

$\displaystyle \lim_{x \to \infty }\frac{x^{3}+4x^{2}+6}{3x^{2}+2x-1}=\displaystyle \lim_{x \to \infty }\frac{\frac{x^{3}}{x^{3}}+\frac{4x^{2}}{x^{3}}+\frac{6}{x^{3}}}{\frac{3x^{2}}{x^{3}}+\frac{2x}{x^{3}}-\frac{1}{x^{3}}}$

$=\displaystyle \lim_{x \to \infty }\frac{1+\frac{4}{x}+\frac{6}{x^{3}}}{\frac{3}{x}+\frac{2}{x^{2}}-\frac{1}{x^{3}}}$

$=\frac{1+0+0}{0+0-0}=\frac{1}{0}=\infty$

Cara 2 : Menggunakan rumus

Bentuk $\displaystyle \lim_{x \to \infty }\frac{x^{3}+4x^{2}+6}{3x^{2}+2x-1}$ memiliki pangkat variabel tertinggi pembilang lebih besar dari pangkat variabel tertinggi penyebut, maka berdasarkan rumus diatas diperoleh :

$\displaystyle \lim_{x \to \infty }\frac{x^{3}+4x^{2}+6}{3x^{2}+2x-1}=\infty$

Pembahasan soal nomor 4 s.d 6 diserahkan ke pembaca dengan berpedoman pada penyelesaian soal nomor 1 sd 3. Sebagai acuan diberikan kunci jawaban untuk soal nomor 4 s.d. 6 sebagai berikut.

4. $\displaystyle \lim_{x \to \infty }\frac{3x^{3}-2x^{2}}{2x^{3}+x}=\frac{3}{2}$

5. $\displaystyle \lim_{x \to \infty }\frac{x^{3}-x}{2x^{4}+1}=0$

6. $\displaystyle \lim_{x \to \infty }\frac{2x^{5}+x^{3}}{x^{3}-x^{2}+1}=\infty$

2. Menyelesaikan Bentuk f(x) - g(x)

Jika $f(x)=\sqrt{ax^{2}+bx+c}$ dan $g(x)=\sqrt{px^{2}+qx+r}$ dengan $a\neq 0 \, \textrm{dan} \, p\neq 0$ , maka untuk menentukan nilai dari $\displaystyle \lim_{x \to \infty }(f(x)-g(x))$ bisa menggunakan dua cara yaitu.

1. Mengalikan dengan pembagian bentuk sekawannya yaitu

$\displaystyle \lim_{x \to \infty }\left ( \sqrt{ax^{2}+bx+c}-\sqrt{px^{2}+qx+r} \right ).\frac{\sqrt{ax^{2}+bx+c}+\sqrt{px^{2}+qx+r}}{\sqrt{ax^{2}+bx+c}+\sqrt{px^{2}+qx+r}}$

2. Menggunakan rumus

Jika a = p maka $\displaystyle \lim_{x \to \infty }f(x)-g(x)=\frac{b-p}{2\sqrt{a}}$

Jika a > p maka $\displaystyle \lim_{x \to \infty }f(x)-g(x)=\infty$

Jika a < p maka $\displaystyle \lim_{x \to \infty }f(x)-g(x)=-\infty$

jika a = p dan b = q maka $\displaystyle \lim_{x \to \infty }f(x)-g(x)=0$

Contoh Soal dan Pembahasan

Hitunglah nilai dari

a. $\displaystyle \lim_{x \to \infty }\left ( 2x-\sqrt{4x^{2}-x} \right )$

b. $\displaystyle \lim_{x \to \infty }\sqrt{x(4x+5)}-\sqrt{4x^{2}-3}$

c. $\displaystyle \lim_{x \to \infty }\sqrt{(x+4)}-\sqrt{2x+1}$

d. $\displaystyle \lim_{x \to \infty }\left [ (2x-1)-\sqrt{4x^{2}-6x-5} \right ]$

Pembahasan

a. $\displaystyle \lim_{x \to \infty }\left ( 2x-\sqrt{4x^{2}-x} \right )$

Cara 1 : dengan mengalikan pembagian bentuk sekawan

$\displaystyle \lim_{x \to \infty }\left ( 2x-\sqrt{4x^{2}-x} \right )=\displaystyle \lim_{x \to \infty }\left ( 2x-\sqrt{4x^{2}-x} \right ).\frac{\left ( 2x+\sqrt{4x^{2}-x} \right )}{\left ( 2x+\sqrt{4x^{2}-x} \right )}$

$=\displaystyle \lim_{x \to \infty }\frac{4x^{2}-(4x^{2}-x)}{2x+\sqrt{4x^{2}-x}}$

$=\displaystyle \lim_{x \to \infty }\frac{x}{2x+\sqrt{4x^{2}-x}}$

Ambil pangkat tertinggi

$=\displaystyle \lim_{x \to \infty }\frac{x}{2x+2x}$

$=\displaystyle \lim_{x \to \infty }\frac{x}{4x}=\frac{1}{4}$

Cara 2 : Menggunakan rumus

$\displaystyle \lim_{x \to \infty }\left ( 2x-\sqrt{4x^{2}-x} \right )=\displaystyle \lim_{x \to \infty }\left ( \sqrt{4x^{2}}-\sqrt{4x^{2}-x} \right )$

Dari bentuk diatas diperoleh a = 4, b = 0, c = 0, p = 4, q = -1 dan r = 0 sehingga diperoleh

$\displaystyle \lim_{x \to \infty }\left ( \sqrt{4x^{2}}-\sqrt{4x^{2}-x} \right )=\frac{b-q}{2\sqrt{a}}$

$=\frac{0-(-1)}{2\sqrt{4}}=\frac{1}{4}$

b. $\displaystyle \lim_{x \to \infty }\sqrt{x(4x+5)}-\sqrt{4x^{2}-3}$

Cara 1 : Mengalikan dengan pembagian bentuk sekawan

$\displaystyle \lim_{x \to \infty }\sqrt{x(4x+5)}-\sqrt{4x^{2}-3}$

$=\displaystyle \lim_{x \to \infty }\sqrt{x(4x+5)}-\sqrt{4x^{2}-3}.\frac{\sqrt{x(4x+5)}+\sqrt{4x^{2}-3}}{\sqrt{x(4x+5)}+\sqrt{4x^{2}-3}}$

$=\displaystyle \lim_{x \to \infty }\frac{(4x^{2}+5x)-(4x^{2}-3)}{\sqrt{(4x^{2}+5x)}+\sqrt{4x^{2}-3}}$

$=\displaystyle \lim_{x \to \infty }\frac{5x+3}{\sqrt{(4x^{2}+5x)}+\sqrt{4x^{2}-3}}$

Ambil pangkat tertinggi

$=\displaystyle \lim_{x \to \infty }\frac{5x}{2x+2x}$

$=\frac{5}{4}$

Cara 2 : Menggunakan rumus

$\displaystyle \lim_{x \to \infty }\sqrt{x(4x+5)}-\sqrt{4x^{2}-3}=\displaystyle \lim_{x \to \infty }\sqrt{(4x^{2}+5x)}-\sqrt{4x^{2}-3}$

Diketahui a = 4, b = 5, c = 0, p = 4, q = 0 dan r = -3 maka

$\displaystyle \lim_{x \to \infty }\sqrt{(4x^{2}+5x)}-\sqrt{4x^{2}-3}=\frac{b-q}{2\sqrt{a}}$

$=\frac{5-0}{2\sqrt{4}}=\frac{5}{4}$

c. $\displaystyle \lim_{x \to \infty }\sqrt{(x+4)}-\sqrt{2x+1}$

Cara 1 : Mengalikan dengan pembagian bentuk sekawan

$\displaystyle \lim_{x \to \infty }\sqrt{(x+4)}-\sqrt{2x+1}$

$=\displaystyle \lim_{x \to \infty }\sqrt{(x+4)}-\sqrt{2x+1}.\frac{\sqrt{(x+4)}+\sqrt{2x+1}}{\sqrt{(x+4)}+\sqrt{2x+1}}$

$=\displaystyle \lim_{x \to \infty }\frac{(x+4)-(2x+1)}{\sqrt{(x+4)}+\sqrt{2x+1}}$

$=\displaystyle \lim_{x \to \infty }\frac{-x+3}{\sqrt{(x+4)}+\sqrt{2x+1}}=\frac{-1}{0}=\infty$

Cara 2 : Menggunakan rumus

Dari bentuk $\displaystyle \lim_{x \to \infty }\sqrt{(x+4)}-\sqrt{2x+1}$

Diketahui : a = 0, b = 1, c = 4, p = 0, q = 2 dan r = 1 sehingga diperoleh

$\displaystyle \lim_{x \to \infty }\sqrt{(x+4)}-\sqrt{2x+1}=\frac{b-q}{2\sqrt{a}}$

$=\frac{1-2}{2\sqrt{0}}=\frac{-1}{0}=\infty$

d. $\displaystyle \lim_{x \to \infty }\left [ (2x-1)-\sqrt{4x^{2}-6x-5} \right ]$

Cara 1 : Mengalikan dengan pembagian bentuk sekawan

$\displaystyle \lim_{x \to \infty }\left [ (2x-1)-\sqrt{4x^{2}-6x-5} \right ]$

$=\displaystyle \lim_{x \to \infty }\left [ (2x-1)-\sqrt{4x^{2}-6x-5} \right ].\frac{(2x-1)+\sqrt{4x^{2}-6x-5}}{(2x-1)+\sqrt{4x^{2}-6x-5}}$

$=\displaystyle \lim_{x \to \infty }\frac{(2x-1)^{2}-(4x^{2}-6x-5)}{(2x-1)+\sqrt{4x^{2}-6x-5}}$

$=\displaystyle \lim_{x \to \infty }\frac{4x^{2}-4x+1-4x^{2}+6x+5}{(2x-1)+\sqrt{4x^{2}-6x-5}}$

$=\displaystyle \lim_{x \to \infty }\frac{2x+6}{(2x-1)+\sqrt{4x^{2}-6x-5}}$

$=\displaystyle \lim_{x \to \infty }\frac{2x}{2x+2x}=\frac{2}{4}=\frac{1}{2}$

Cara 2 : Menggunakan rumus

$\displaystyle \lim_{x \to \infty }\left [ (2x-1)-\sqrt{4x^{2}-6x-5} \right ]=\displaystyle \lim_{x \to \infty }\left [ (\sqrt{(2x-1)^{2}}-\sqrt{4x^{2}-6x-5} \right ]$

$=\displaystyle \lim_{x \to \infty }\left [ (\sqrt{4x^{2}-4x+2}-\sqrt{4x^{2}-6x-5} \right ]$

Dari bentuk ini diperoleh a = 4, b = -4 c = 2, p = 4, q = -6 dan r = -5 sehingga diperoleh

$\displaystyle \lim_{x \to \infty }\left [ (2x-1)-\sqrt{4x^{2}-6x-5} \right ]=\frac{b-q}{2\sqrt{a}}$

$=\frac{-4-(-6)}{2\sqrt{4}}$

$=\frac{2}{4}=\frac{1}{2}$

Demikian pembahasan tentang menentukan limit tak hingga dan limit di tak hingga pada fungsi aljabar, semoga pembahasan ini bermanfaat, dan terimakasih.

Limit Tak Hingga dan Limit di Tak Hingga dan Pembahasan Soal

A. Limit Tak Hingga **(infinity limits)**

**B. Limit di Tak Hingga (limits at infinity)**

C. Menenetukan nilai limit di tak hingga pada fungsi aljabar

Contoh Soal dan Pembahasan

2. Menyelesaikan Bentuk f(x) - g(x)

Contoh Soal dan Pembahasan

Post a Comment

إرسال تعليق

نموذج الاتصال

Limit Tak Hingga dan Limit di Tak Hingga dan Pembahasan Soal

A. Limit Tak Hingga (infinity limits)

B. Limit di Tak Hingga (limits at infinity)

C. Menenetukan nilai limit di tak hingga pada fungsi aljabar

Contoh Soal dan Pembahasan

2. Menyelesaikan Bentuk f(x) - g(x)

Contoh Soal dan Pembahasan

You might like

Post a Comment

إرسال تعليق

نموذج الاتصال

A. Limit Tak Hingga **(infinity limits)**

**B. Limit di Tak Hingga (limits at infinity)**