Pembahasan Soal Penilaian Akhir Semester (PAS) Matematika Wajib Kelas 12 SMA/MA Tahun 2021.
1. Perhatikan kubus ABCD.EFGH berikut
Pasangan titik-titik yang memiliki jarak terjauh adalah....
A. AG, CE, BH, dan DF
B. AG, AC, EG, dan DH
C. AC, AF, BH, dan AE
D. BC, CH, DF, dan CG
E. AH, BG, CH, dan DG
Pembahasan
Titik-titik yang memiliki jarak terjauh dari kubus diatas adalah titik-titik yang membentuk diagonal ruang. Dari gambar diatas pasangan titik yang memiliki jarak terjauh adalah AG, CE, BH, dan DF.
Kunci Jawaban : A
2. Sebuah kubus ABCD.EFGH dengan panjang rusuk 10 cm, maka jarak titik D ke titik F adalah....
C. 10
Pembahasan
Cara 1
Langkah-langkah menentukan jarak titik D ke titik F
1. Gambarlah kubus ABCD.EFGH
2. Buat ruas garis dari titik D ke titik F, seperti gambar berikut
4. Misal ambil segitiga DHF. Perhatikan segitiga DHF.
Dengan menggunakan teorema pythagoras akan dicari panjang HF dari segitiga FGH
Dari segitiga DHF akan dicari panjang DF
Jadi jarak titik D ke titik F adalah cm
Cara 2
Garis DF merupakan diagonal ruang kubus ABCD.EFGH
Kunci Jawaban : E
Soal 2
3. Perhatikan balok ABCD.EFGH berikut.
Jika panjang AB = 8 cm, AD = 4 cm, CG = 6 cm dan titik P di tengah-tengah rusuk BC, maka jarak titik A dan titik P adalah ....
A.
B.
C.
D.
E.
Pembahasan
Gambar balok dari soal diatas adalah
Jarak titik A ke titik P adan panjang ruas garis AP. Untuk mencari panjang AP perhatikan segitiga ABP.
BC = AD = 4
BP = 1/2 BC = 1/2 . 4 = 2
Dengan menggunakan teorema pythagoras diperoleh :
Jadi jarak titik A ke titik P adalah cm
Kunci Jawaban : B
Soal 3
Sebuah limas beraturan T.ABCD dengan panjang rusuk alas 6 cm dan panjang AT = 12 cm, jarak titik A dan garis CT adalah ....
A.
B.
C.
D.
E.
Pembahasan
Gambar dari limas beraturan pada soal adalah
Proyeksi/bayangan titik A pada garis CT adalah titik P sehingga AP tegak lurus CT, maka jarak titik A ke garis CT adalah ruas garis AP.
Perhatikan segitiga ACT
Akan dicari panjang AC. Karena AC merupakan diagonal bidang alas maka
AC =
Dari segitiga AOT, akan dicari tinggi limas yaitu OT
Dengan menggunakan kesamaan luas segitiga dari segitiga ACT diperoleh
Jadi jarak titik A ke garis CT adalah cm
Kunci Jawaban : D
Soal 4
Sebuah kubus ABCD.EFGH dengan panjang rusuk 4 cm. Jika titik P terletak ditengah-tengah rusuk BC, maka jarak titik P ke garis EH adalah ....
A.
B.
C.
D.
E.
Pembahasan
Gambar kubus dari soal diatas adalah
Proyeksi/bayangan titik P pada garis EH adalah titik Q, sehingga PQ tegak lurus EH, maka jarak titik P ke garis EH adalah panjang ruas garis PQ. Untuk mencari panjang ruas garis PQ, buat sebuah segitiga dari garis PQ yaitu segitiga PRQ yang merupakan segitiga siku-siku dan diperoleh :
Jadi jarak titik P ke garis EH adalah cm.
Kunci Jawaban : B
Soal 5
Sebuah balok ABCD.EFGH dengan panjang AB = 4 cm, BC = 3 cm dan CG = 6 cm. Jarak titik B dan bidang ACGE adalah ....
A.
B.
C.
D.
E.
Pembahasan
Gambar balok pada soal diatas adalah
Proyeksi/bayangan titik B pada bidang ACGE adalah titik P yang terletak pada garis AC, sehingga BP tegaklurus AC, maka jarak titik B ke bidang ACGE adalah panjang ruas garis BP.
Untuk mencari panjang BP perhatikan segitiga siku-siku ABC.
Akan dicari panjang AC
Dengan menggunakan kesamaan luas segitiga dari segitiga ABC diperoleh
Jadi jarak titik B ke bidang ACGE adalah
Kunci Jawaban : C
Soal 6
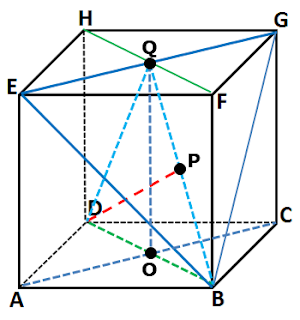
Sebuah kubus ABCD.EFGH dengan panjang rusuk 8 cm. Jarak titik D dan bidang BEG adalah ....
A.
B.
C.
D.
E.
Pembahasan
Gambar kubus dari soal diatas adalah
Buatlah sebuah bidang yang memotong bidang BEG pada garis BQ yaitu bidang BDHF dan melalui titik D.
Proyeksi titik D pada garis BQ adalah titik P sehingga DP tegak lurus BQ, maka jarak titik D ke garis BQ adalah panjang ruas garis DP.
Panjang ruas garis DP juga merupakan jarak titik D ke bidang BEG.
Untuk menentukan panjang dari ruas garis DP buatlah segitiga dari garis BQ yaitu segitiga BDQ.
Tarik garis OQ merupakan tinggi dari segitiga BDQ.
Perhatikan segitiga BDQ.
BD =
OQ = 8
Akan dicari panjang BQ dari segitiga BOQ
Sehingga diperoleh
Dengan menggunakan kesamaan luas segitiga dari segitiga BDQ diperoleh :
Jadi jarak titik D ke bidang BEG adalah cm
Kunci Jawaban : B
Soal 7
Perhatikan gambar kubus ABCD.EFGH berikut
Pasangan rusuk kubus yang saling bersilangan adalah....
A. Rusuk EF dan rusuk AD
B. Rusuk BC dan rusuk AD
C. Rusuk AE dan rusuk DH
D. Rusuk AB dan rusuk BF
E. Rusuk CG dan rusuk AE
Kunci Jawaban : A
Soal 9
Diketahui kubus ABCD.EFGH dengan panjang rusuk 10 cm, maka jarak garis BE ke garis DG adalah ....
A.
B.
C. 10
D.
E.
Pembahasan
Gambar kubus ABCD.EFGH dari soal diatas adalah :
Proyeksi garis BE pada bidang CDHG adalah garis CH dan proyeksi garis DG pada bidang ABFE adalah garis AF. Titik potong garis BE dan AF adalah titik P. Proyeksi titik P pada garis DG adalah Q, sehingga PQ tegaklurus BE dan DG, maka jarak garis BE dan garis DG adalah panjang ruas garis PQ.
PQ = panjang rusuk kubus = 10 cm
Kunci Jawaban : C
Soal 10
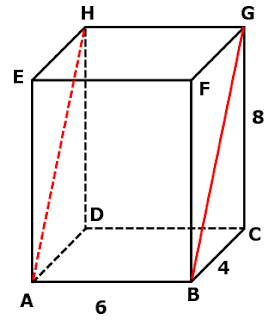
Sebuah Balok ABCD.EFGH dengan ukuran 6 cm x 4 cm x 8 cm. Jarak garis AB ke garis GH adalah ....
A.
B.
C. 10
D.
E.
Pembahasan
Gambar balok dari soal diatas adalah
Jarak garis AB ke garis GH adalah panjang ruas garis AH atau BG. Ambil salah satu, misal ruas garis BG.
Dari garis BG ambil segitiga BCG atau segitiga BFG, misal segitiga BCG.
Dengan menggunakan teorema pythagoras diperoleh panjang BG yaitu
Jadi jarak garis AB ke garis GH adalah cm
Kunci Jawaban : D
Soal 11
Perhatikan kubus ABCD. EFGH berikut.
Garis yang bersilangan tegaklurus dengan bidang AFH adalah ....
A. BD
B. DG
C. EG
D. AC
E. AE
Pembahasan
Gambar kubus dari soal diatas adalah
Gambar bidang yang melalui garis BD dan sejajar bidang AFH yaitu bidang BDG. Gambar bidang yang memotong bidang AFH dan BDG sehingga garis potong AI sejajar dengan garis AI // JG. Garis JG tegak lurus BD, sehigga garis BD bersilangan tegak lurus dengan bidang AFH.
Kunci Jawaban : A
Soal 12
Sebuah limas beraturan T.ABCD dengan panjang rusuk alas 12 cm dan tinggi = 8 cm. Jarak garis CD dan bidang TAB adalah .... cm
A.
B.
C.
D.
E. 15
Pembahasan
Gambar limas beraturan dari soal diatas adalah
Proyeksi garis CD pada bidang TAB adalah garis QR. Pilih titik Q, proyeksi titik Q pada garis CD adalah titik P, sehingga jarak garis CD ke bidang TAB adalah panjang ruas garis PQ.
Untuk memudahkan dalam menghitung panjang PQ buat garis sejajar PQ yang melalui titik tengah CD dan titik G pada garis TE, yaitu garis FG.
Perhatikan segitiga TEF
Akan dicari panjang TE dari segitiga TOE
OE = 1/2 FE = 1/2 . 12 = 6
= 10
Dengan menggunakan kesamaan luas segitiga dari segitiga TEF diperoleh
Jadi jarak garis CD ke bidang TAB adalah cm
Kunci Jawaban : D












izin copy buat bahan PAS ya... terimakasih
ReplyDeletePost a Comment
Terimakasih untuk anda telah berkomentar di postingan ini