Ragam dan Simpangan Baku (Standar Deviasi) Dari Distribusi Frekuensi Data Kelompok

Nurman Karim August 24, 2021 0

Ragam adalah ukuran seberapa jauh sebuah kumpulan bilangan tersebar. Ragam selalu bernilai non-negatif. Ragam nol mengindikasikan bahwa semua nilai sama. Ragam yang rendah mengindikasikan bahwa titik data condong sangat dekat dengan nilai rerata (nilai ekspektasi) dan antara satu sama lainnya, sementara ragam yang tinggi mengindikasikan bahwa titik data sangat tersebar disekitar rerata dan dari satu sama lainnya.

Pengukuran yang sama yaitu akar kuadrat dari ragam, disebut juga simpangan baku (SD).

Untuk menghitung ragam digunakan rumus:

Rumus ragam

Gambar 1. Rumus Ragam

Keterangan

$x_{i}$ = nilai tengah kelas ke-i

$\overline{x}$ = nilai rata-rata

$\sum f_{i}$ = n = banyak data

Untuk menghitung Standar Deviasi digunakan rumus.

$SD=\sqrt{\frac{\sum f_{i}\left ( x_{i}-\overline{x} \right )^{2}}{\sum f_{i}}}$

Contoh Soal 1

Hitung ragam dan simpangan baku dari data berikut.

Pembahasan

Tabel diatas diubah menjadi tabel berikut

Nilai Rata-rata = $\overline{x}=\frac{\sum x_{i}f_{i}}{\sum f_{i}}$

$=\frac{1020}{30}$

$=34$

Keterangan perhitungan tabel

$x_{i}$ = (21+25/2 = 46/2 = 23 dan seterusnya

$x_{i}f_{i}$ = 23 . 2 = 46 dan seterusnya

$x_{i}-\overline{x}$ = 23 - 34 = -11 dan seterusnya

$(x_{i}-\overline{x})^{2}$ = (-11) . (-11) = 121 dan seterusnya

$f_{i}(x_{i}-\overline{x})^{2}$ = 2 . 121 = 242 dan seterusnya

Maka kita bisa menghitung nilai yang ditanyakan yaitu.

$Ragam = \frac{\sum f_{i}\left ( x_{i}-\overline{x} \right )^{2}}{\sum f_{i}}$

$=\frac{1270}{30}$

$=42,33$

dan

$SD=\sqrt{\frac{\sum f_{i}\left ( x_{i}-\overline{x} \right )^{2}}{\sum f_{i}}}$

$=\sqrt{\frac{1270}{30}}$

$=\sqrt{42,33}$

$=6,51$

Contoh Soal 2

Tentukan standar deviasi dari data pada tabel berikut.

Pembahasan

Tabel diatas diubah menjadi tabel berikut ini.

Dari tabel diatas dapat dihitung :

Mean = $\overline{x}=\frac{\sum x_{i}f_{i}}{\sum f_{i}}$

$=\frac{3725}{50}$

$=74,50$

Maka dapat dihitung nilai standar deviasinya yaitu

$SD=\sqrt{\frac{\sum f_{i}\left ( x_{i}-\overline{x} \right )^{2}}{\sum f_{i}}}$

$=\sqrt{\frac{7400}{50}}$

$=\sqrt{148}$

$=12,17$

Contoh Soal 3

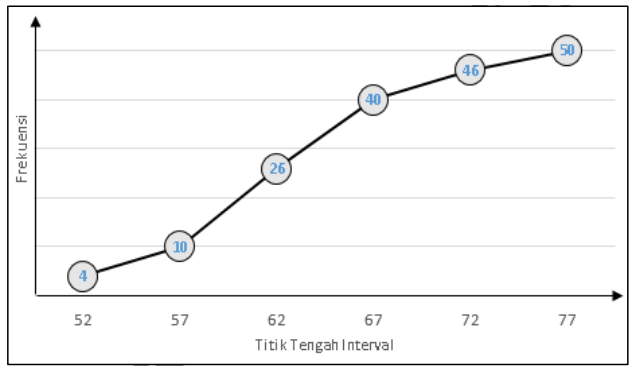
Hitunglah standar deviasi dari data yang disajikan dalam ogive berikut.

Ogive

Pembahasan

Ogive diatas diubah menjadi tabel distribusi frekuensi berikut

Keterangan perhitungan pada tabel

Perhitungan menentukan interval kelas

Pada kelas ke-1 titik tengah 52 dan kelas ke-2 titik tengahnya 57, maka

Panjang kelas = 57 - 52 = 5

Nilai pada kelas ke-1 adalah 50, 51, 52, 53, 54 sehingga intervalnya 50 - 54.

Untuk interval kelas selanjutnya perhitungannya diserahkan ke pembaca dan hasilnya seperti pada tabel diatas.

Perhitungan Frekuensi

Frekuensi kelas ke-1

= frekuensi kumulatifnya = 4

Frekuensi kelas ke-2 = Fk2 - f1

= 10 - 4 = 6

Frekuensi kelas ke-3

= Fk3 - (f1 + f2)

= 26 - (4 + 6) = 26 - 10 = 16

Frekuensi kelas ke -4

= Fk4 - (f1+f2+f3)

= 40 - (4+6+16)

= 40 - 26 = 14

Frekuensi kelas ke-5 dan ke-6 perhitungan diserahkan ke pembaca dan hasilnya seperti pada tabel diatas.

Perhitungan nilai rata-rata sebagai berikut

Mean = $\overline{x}=\frac{\sum x_{i}f_{i}}{\sum f_{i}}$

$=\frac{3220}{50}$

Sehingga perhitungan standar deviasinya sebagai berikut

$SD=\sqrt{\frac{\sum f_{i}\left ( x_{i}-\overline{x} \right )^{2}}{\sum f_{i}}}$

$=64,4$

$=\sqrt{\frac{2112}{50}}$

$=\sqrt{42,24}$

$=6,50$

Post a Comment

Terimakasih untuk anda telah berkomentar di postingan ini